Grafen in Sage: Euleriaanse grafen en circuits
Sage heeft heel wat mogelijkheden voor het werken met grafen. Je kan een graaf met $n$ toppen maken via de functie Graph, en er dan bogen aan toevoegen. In deze functie kan je ook meer informatie meegeven, zoals de adjacentiematrix of een dictionary met lijsten die voor elke top de buren geeft.
|
|
Je kan ook heel wat standaardgrafen automatisch laten genereren in Sage: het object graphs heeft hiervoor allerlei functies.
|
Oplossing 1
Hieronder vind je drie mogelijkheden voor het implementeren van is_euleriaans. Deze zijn uiteraard niet de enige mogelijkheden.
|
|
|
|
|
|
Ter controle moet je functie de volgende resultaten geven:
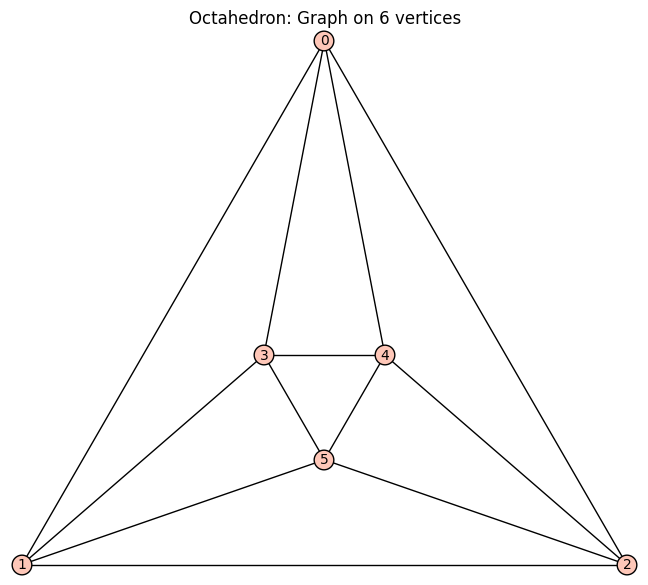
Graph on 5 vertices is euleriaans. Mijn functie geeft True Complete graph is euleriaans. Mijn functie geeft True Octahedron is euleriaans. Mijn functie geeft True Petersen graph is niet euleriaans. Mijn functie geeft False Complete bipartite graph is niet euleriaans. Mijn functie geeft False Graph on 5 vertices is euleriaans. Mijn functie geeft True Complete graph is euleriaans. Mijn functie geeft True Octahedron is euleriaans. Mijn functie geeft True Petersen graph is niet euleriaans. Mijn functie geeft False Complete bipartite graph is niet euleriaans. Mijn functie geeft False |
Opdracht 2
Het bewijs van stelling 3.2.3 geeft een methode om van een Euleriaanse graaf een Euleriaans circuit te bepalen, het algoritme van Fleury. Hieronder vind je een implementatie van fleury.
|
|
Om je functie te testen is geeft de volgende functie je een manier om het gevonden circuit interactief weer te geven.
|
|
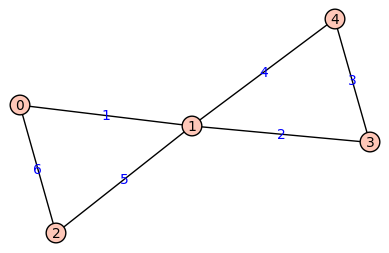
Om je functie te testen is geven we je de volgende functies om het gevonden circuit interactief weer te geven.
Click to the left again to hide and once more to show the dynamic interactive window |
|||||||||||||||||
|
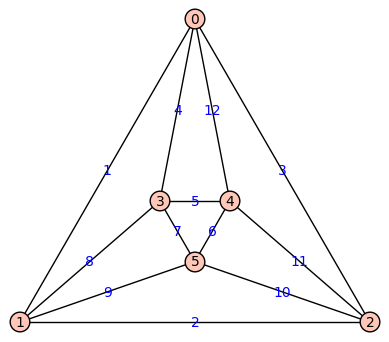
Click to the left again to hide and once more to show the dynamic interactive window |
|||||||||||||||||
|
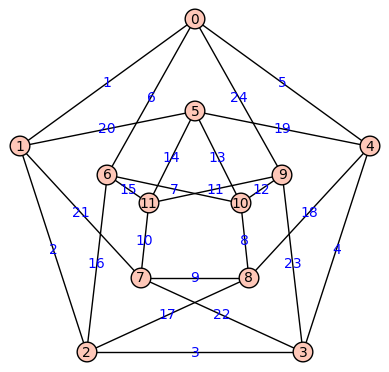
Click to the left again to hide and once more to show the dynamic interactive window |
|||||||||||||||||
|
|
|