Defineer de matrices $\mathbf{H}$ en $\mathbf{S}$, door middel van hun matrixelementen, waarvoor de integralen zijn meegegeven in vergelijkingen (20) en (21).
|
def H11(R,V0) : return -0.5*V0*(1+2.0*exp(-4.0*V0*R))+V0^2*kronecker_delta(2*R,0.)*exp(2*R*V0)
def H12(R,V0) : return -0.5*V0*(3.0+V0*R)*exp(-2.0*V0*R)+V0^2*kronecker_delta(2*R,0.)
def S11(R,V0) : return 1.0
def S12(R,V0) : return (1.0+V0*R)*exp(-2.0*V0*R)
|
|
De matrices worden geconstrueerd uit hun matrixelementen, opnieuw, bemerk de symmetrie. MH staat voor de matrix $\mathbf{H}$ vergelijking (21), MS staat voor de matrix $\mathbf{S}$ vergelijking (23) en MT staat voor de karakteristieke matrix $\mathbf{H}-\mathbf{S}$, waarvoor we de basis willen te weten komen waarbinnen de matrix MT diagonaal is.

|
def MH(R,V0) : return matrix(RDF,2,2,[H11(R,V0),H12(R,V0),H12(R,V0),H11(R,V0)])
def MS(R,V0) : return matrix(RDF,2,2,[S11(R,V0),S12(R,V0),S12(R,V0),S11(R,V0)])
def MT(R,V0) : return MH(R,V0)-MS(R,V0)
|
|
dBij wijze van voorbeeld, de waardes voor de matrixelementen van de matrix MH,MS en MT op het punt $(1.0,1.0)$
|
show(MH(1.,1.));show(MS(1.,1.));show(MT(1.,1.));
show(MH(0.,1.));show(MS(0.,1.));show(MT(0.,1.));
|
|
Deze matrix MT moet gediagonaliseerd worden, of - met andere woorden - we moeten zoeken naar de eigenwaarden en de bijhorende eigenvectoren. De eigenwaarden leren ons de energie\"en van het probleem waarvoor we op zoek waren naar het minimum. Zo kunnen we bijvoorbeeld de energie-waarden berekenen voor het geval waar beide kernen op een afstand 2.0 van elkaar zijn verwijderd. Voor elke afstand tussen de beide kernen verkrijgen we andere eigenwaarden/energiewaarden

|
def eigvl(R,V0) :return MT(R,V0).eigenvalues()
show(eigvl(5.,1.))
|
|
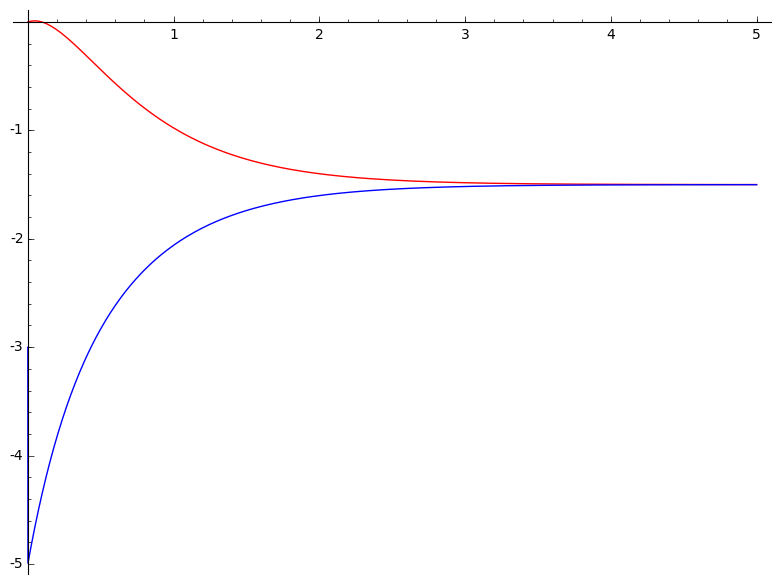
Zoals kan berekend worden, en zoals te zien op onderstaande plot, krijg je een (a-?)typisch bindend en anti-bindend gedrag. Deze plot is gegenereerd voor $V_0=1.0$
|
def firsteig(R) : return eigvl(R,1.)[0];
def secondeig(R) : return eigvl(R,1.)[1];
g = Graphics()
g += plot(firsteig, (R,0,5),color="red")
g += plot(secondeig, (R, 0, 5))
g.show()
|
dDe bijhorende eigenvectoren vertellen ons welke lineaire combinatie van de beide basisfuncties correspondeert met de berekende eigenwaarden.
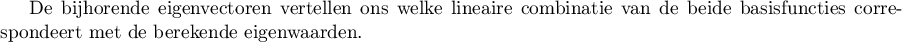
|
D,P = MT(0.5,0.5).eigenmatrix_right()
show(P)
|
|
def phi1(R,V0,x) :return exp(-V0*abs(x-R))
def phi2(R,V0,x) :return exp(-V0*abs(x+R))
|
|
def function1(x) : return (P[0,0]*phi1(0,1.,x)+P[0,1]*phi2(0,1.,x));
def function2(x) : return (P[1,0]*phi1(0,1.,x)+P[1,1]*phi2(0,1.,x));
def function1sq(x) : return (function1(x))^2;
def function2sq(x) : return (function2(x))^2;
g = Graphics()
g += plot(function1, (x,-5,5),color="blue",linestyle="dashed")
g += plot(function2, (x,-5, 5),color="red",linestyle="dashed")
g += plot(function1sq, (x,-5,5),color="blue")
g += plot(function2sq, (x,-5, 5),color="red")
g.show()
|
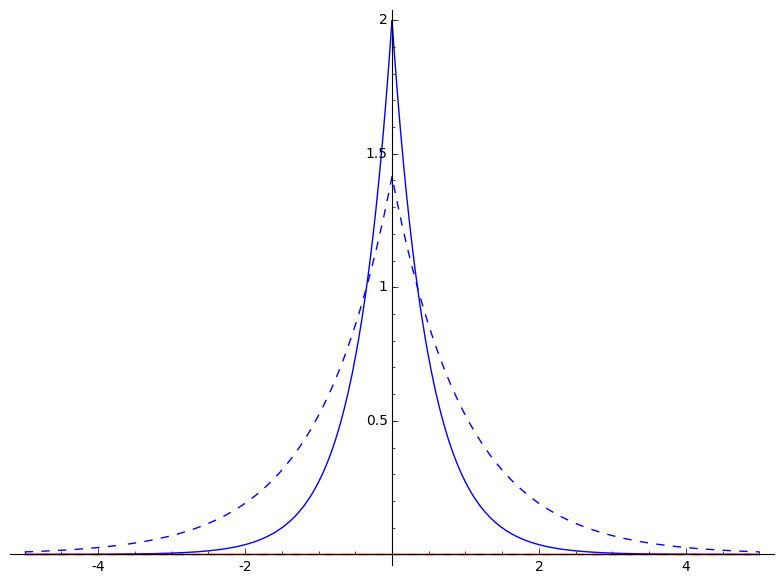
def function1(x) : return (P[0,0]*phi1(0.1,1.,x)+P[0,1]*phi2(0.1,1.,x));
def function2(x) : return (P[1,0]*phi1(0.1,1.,x)+P[1,1]*phi2(0.1,1.,x));
def function1sq(x) : return (function1(x))^2;
def function2sq(x) : return (function2(x))^2;
g = Graphics()
g += plot(function1, (x,-5,5),color="blue",linestyle="dashed")
g += plot(function2, (x,-5, 5),color="red",linestyle="dashed")
g += plot(function1sq, (x,-5,5),color="blue")
g += plot(function2sq, (x,-5, 5),color="red")
g.show()
|
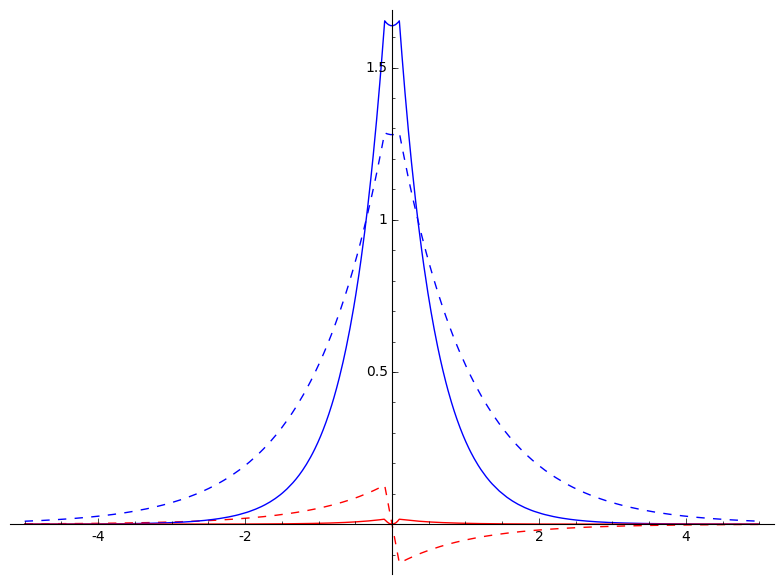
def function1(x) : return (P[0,0]*phi1(1,1.,x)+P[0,1]*phi2(1,1.,x));
def function2(x) : return (P[1,0]*phi1(1,1.,x)+P[1,1]*phi2(1,1.,x));
def function1sq(x) : return (function1(x))^2;
def function2sq(x) : return (function2(x))^2;
g = Graphics()
g += plot(function1, (x,-5,5),color="blue",linestyle="dashed")
g += plot(function2, (x,-5, 5),color="red",linestyle="dashed")
g += plot(function1sq, (x,-5,5),color="blue")
g += plot(function2sq, (x,-5, 5),color="red")
g.show()
|
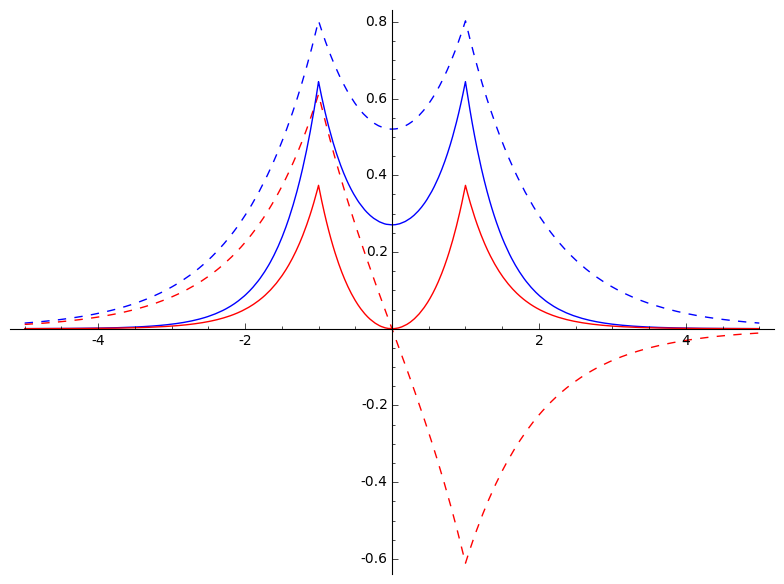
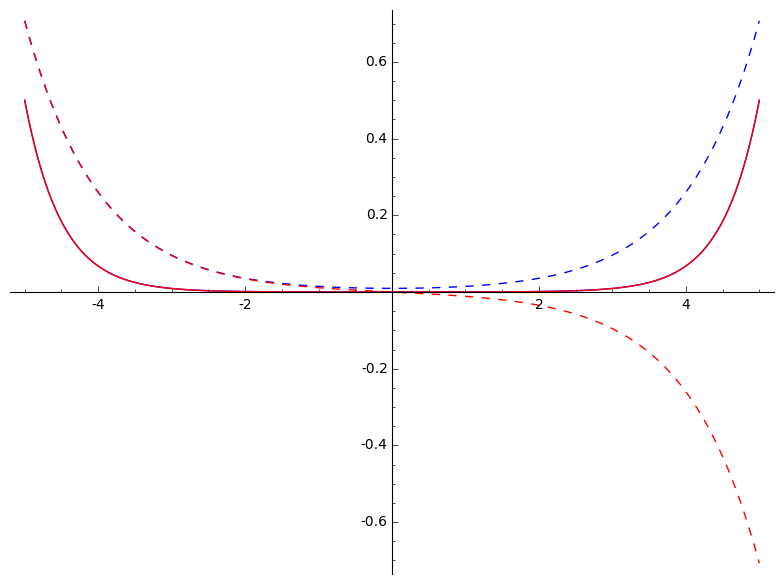
def function1(x) : return (P[0,0]*phi1(5,1.,x)+P[0,1]*phi2(5,1.,x));
def function2(x) : return (P[1,0]*phi1(5,1.,x)+P[1,1]*phi2(5,1.,x));
def function1sq(x) : return (function1(x))^2;
def function2sq(x) : return (function2(x))^2;
g = Graphics()
g += plot(function1, (x,-5,5),color="blue",linestyle="dashed")
g += plot(function2, (x,-5, 5),color="red",linestyle="dashed")
g += plot(function1sq, (x,-5,5),color="blue")
g += plot(function2sq, (x,-5, 5),color="red")
g.show()
|
|
|