CoMa 2016

Vraag 1: Maxwell, Hubble en Newton

We kunnen simpelweg de opgave ingeven in sage:

Deze oplossing is helemaal niet efficiënt of snel. Kunnen we iets slimmer bedenken?

In de volgende som

$ \sum_{x = 0.1,\,0.1+10^{-6}, \dots}^{1.1-10^{-6}} \cos(x - 0.01) - cos(x) $

kunnen we zien dat we steeds tweemaal dezelfde cosinus berekenen (eens in $\cos(x-0.01)$ en eens in $\cos(x)$), dus we kunnen dit efficiënter berekenen:

Vraag 2: "Don't move!"

We noemen het aantal permutaties van $n$ elementen met exact $i$ fixpunten $ d_{n, i} $. Een formule voor $d_{n,i}$ kunnen we recursief opstellen, voor het geval $i = 0$ verwijzen we naar de wikipediapagina.

We kunnen nadenken op welke rechten door $O$ de twee overige fixpunten moeten liggen.

Indien deze twee fixpunten op dezelfde rechte door $O$ liggen kunnen we volgende formule gebruiken:

$ \sum_{i=1}^{n+1} d_{n+1,i} \cdot (n-1)!^{n+1-i} \cdot i \cdot d_{n-1,2} \cdot d_{n-1,0}^{i-1} $

Indien deze twee fixpunten op verschillende rechte door $O$ liggen kunnen we het volgende opstellen:

$ \sum_{i=2}^{n+1} d_{n+1,i} \cdot (n-1)!^{n+1-i} \cdot \frac{i (i-1)}{2} \cdot d_{n-1,1}^2 \cdot d_{n-1,0}^{i-2} $

(In beide sommen stelt $i$ het aantal fixrechten door $O$ voor.)

Vraag 3

Op wikipedia vinden we volgende formule terug:

$ \log n + \log\log n - 1 < \frac{p_n}{n} < \log n + \log \log n \quad\text{for } n \ge 6 $.

Deze kunnen we gebruiken in sage:

Dus de eerste $10$ cijfers zijn $9774265192$.

Vraag 4: Meer te doen dan je ooit raden kon

Voor dit probleem zijn zeker meerdere oplossingen mogelijk. We zullen hier een methode gebruiken die ook zeker toepasbaar is op gelijkende problemen.

Als eerste kunnen we vaststellen dat dit probleem te beschrijven is als een recurrente rij. De volgende observatie is hiervoor noodzakelijk:

$\left(\begin{array}{c} F_n \\  F_{n+1} \\ nF_n \\ nF_{n+1} \\ S(n-1) \end{array}\right)= \left(\begin{array}{rrrrr}0 & 1 & 0 & 0 & 0 \\1 & 1 & 0 & 0 & 0 \\0 & 1 & 0 & 1 & 0 \\1 & 1 & 1 & 1 & 0 \\0 & 0 & 1 & 0 & -1\end{array}\right)  \left(\begin{array}{c} F_{n-1} \\  F_n \\ (n-1)F_{n-1} \\ (n-1)F_n \\ S(n-2) \end{array}\right)$

Om nu $S(n)$ voor een grote $n$ te berekenen is het voldoende deze matrix tot de macht $n$ te verheffen, dit kan sage zeer efficiënt.

Vraag 5: PRIME's great hall

Een discrete oplossing is wiskundig minder interessant. Het is voldoende om een 300 bij 300 rooster te leggen over $[-\pi, 0] \times [0,\pi]$. Op dit rooster kunnen we dan via dynamisch programmeren een route vinden die roosterpunten verbindt en de oppervlakte van het gordijn minimaliseert. Dit geeft na een tiental seconden (op een modern systeem) een antwoord van $16.5344$.

Om een analytische oplossing te bekomen gaan we de Euler-Lagrange vergelijking gebruiken. Ook is ervoor gezorgd dat al het (symbolisch) rekenwerk door sage gebeurt.

We beginnen met het pad dat we afleggen in het XY-vlak te beschrijven door $(x, g(x))$, waarbij $g$ een algemene (onbekende) functie is.

De Euler-Lagrange-vergelijking gaat opzoek naar een extremum van:

$\int_a^b L(x, y, y') dx$ voor een $L$. Dus in ons geval:

$L(x, y, y') = (2+\cos(y))\sqrt{1+y'^2} dx$

De verglijking zegt dat het nodig is dat:

$L_y - \frac{d}{dx}L_{y'}(x, y, y') = 0$

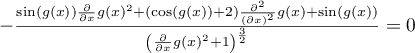
Dit is de nodige voorwaarde die uit de Euler-Lagrange-vergelijking volgt.  Het is dus nodig dat

$\sin(g)(1+ g'^2) + (\cos(g)+2) g'' = 0$

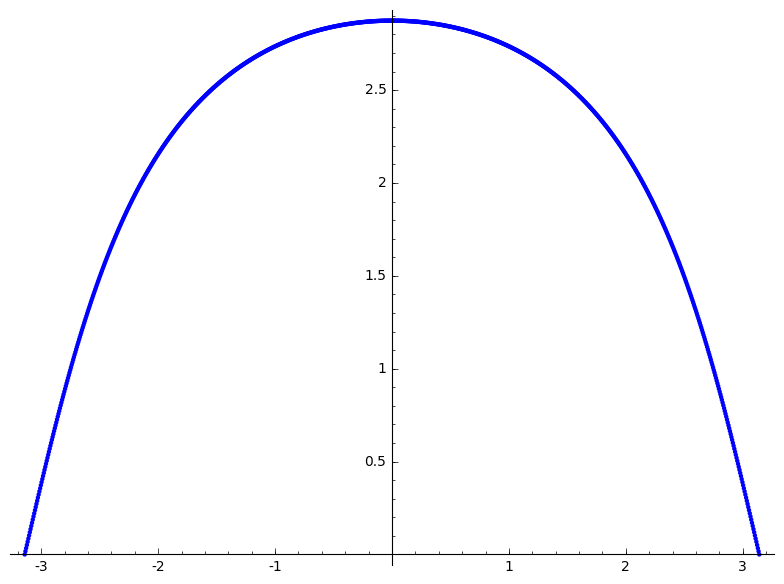
Deze differentiaalvergelijking kunnen we via sage-numeriek oplossen als we er een stelsel van eerste orde differentiaalvergelijkingen van maken. Een kleine moeilijkheid is dat we niet echt een beginvoorwaarde hebben. We weten dat $g(-\pi) = g(\pi) = 0$, maar hier kunnen we numeriek niet echt iets mee doen. We hebben $g'(-\pi)$ nodig, via een paar plotjes weten we dat die minstens $2.5$ en maximaal $2.8$ moet zijn. We kunnen dus naar de juiste $g'(-\pi)$ waard gaan door te eisen dat $g(\pi) = 0$ door deze voor verschillende $g'(-\pi)$ waarden te berekenen. (find_root doet dit).

Deze grafiek sluit aan bij de intuïtie die we hadden over het probleem. Nu moeten we deze gevonden functie nog invullen in de integraal die we wouden minimaliseren.

$16.5337$ sluit aan bij de oplossing die we gevonden hadden bij het discretiseren. En omdat er naar twee decimalen was gevraagd geven beide methoden $16.53$ als correcte antwoord.