CoMa 2017 Antwoorden

1  Wederom heeft Toon (on)gelijk

Toon beweert dat er nog nooit tweemaal hetzelfde spel manillen is gespeeld.

Manillen is een kaarspel met vier spelers en 32 kaarten. Elke speler krijgt acht kaarten in zijn hand. Eén voor één legt een speler een kaart neer om de slag te halen. We zeggen dat twee spelletjes hetzelfde zijn als er bij de start exact dezelfde handen in dezelfde volgorde gedeeld werden met eventueel een verschillende beginspeler.

Hoeveel spelletjes moeten er minimaal reeds gespeeld zijn zodat de kans groter is dan $0.1\%$ dat er al minstens tweemaal hetzelfde spel manillen is gespeeld.

Oordeel zelf of de bewering van Toon gestaafd was.

Ten eerste tellen we het aantal mogelijke spellen. Op hoeveel manieren kunnen we 4 spelers elk 8 kaarten uitdelen? Met het multinomiaal getal: $\frac{32!}{8!8!8!8!}$. Zoals de vraag vertelde is de beginspeler van geen belang, dus delen we dit aantal nog door vier: $n = \frac{32!}{4 (8!)^4}$.

We noemen $P(k)$ de kans dat er na $k$ spellen nog nooit twee maal hetzelfde spel is gespeeld. We zien dat $P(0) = 1$ en $P(k) = \frac{n-(k-1)}{n}P(k-1)$. Nu kunnen we simpelweg op zoek gaan naar wanneer $P(k) < 0.999$.

2  Hoezo veel te moeilijk?

Gegeven $f : F^n \to F^n : f(x_1, \dots, x_n) = (x_2 x_3, x_3 x_4, \dots, x_n x_1, x_1 x_2) $.

Omdat $f$ veel te moeilijk is voor ons, zouden we graag deze functie benaderen door een lineaire afbeelding $\hat{f}$. Wel eisen we dat $\hat{f}(\pmb{x}) = f(\pmb{x})$ voor bepaalde $\pmb{x}$ waarden. Naast voor $\pmb{x}=\pmb{0}$ moet ook $\hat{f}(\pmb{x}) = f(\pmb{x})$ voor:

$\pmb{x} \in \left\{\left(p_{i+1}\ ^i,\,p_{i+2}\ ^i,\,\dots,\,p_{i+n}\ ^i\right)\quad|\quad\forall i \in \{1, \dots, m\} \right\}$
met $m$ zo groot mogelijk en $p_k$ het $k^\text{de}$ priemgetal.

Kies $F = F_{29} $ en $n = 100$, wat is dan de som (in $\mathbb{N}$) van de coëficienten van $\hat{f}(1, 2, \dots, n)$?

Noem $\pmb{x_i} = \left(p_{i+1}\ ^i,\,p_{i+2}\ ^i,\,\dots,\,p_{i+n}\ ^i\right)$.

We zijn op zoek naar een lineaire afbeelding $f$, dus naar een matrix $F$ waarvoor $\pmb{x_i} F = f(\pmb{x_i})$ voor $1 \leq i \leq m$. Als we al deze voorwaarden samengieten tot een matrix vergelijking staat er: $X F = f(X)$, met de $i^\text{de}$ rij van $X$ gelijk aan $\pmb{x_i}$ en op de $i^\text{de}$ rij van $f(X)$ staat $f(\pmb{x_i})$. Om $m$ te bepalen kunnen we rijen aan $X$ blijven toevoegen zolang de oplossing niet uniek is, of anders gezegd, zolang de rechter kern dimensie niet $0$ heeft.

3  Bovengemiddeld interessante getallen

We noemen $n$ een bovengemiddeld interessant getal wanneer de volgende waarden gehele getallen zijn:

• het rekenkundig gemiddelde van de delers van $n-1$
• het harmonisch gemiddelde van de delers van $n$
• het meetkundig gemiddelde van de delers van $n+1$

Wat is de som van alle bovengemiddeld interessante getallen kleiner dan $10^{10}$.

De belangerijkste observatie die we moeten maken is dat het meetkundig gemiddelde van de delers van $m$ gelijk is aan $\sqrt{m}$, dit is pas geheel als $m$ een kwadraat is (zie bijvoorbeeld https://oeis.org/A001599/a001599.pdf). Dus we kunnen alle kwadraten kleiner dan $10^{10}$ bekijken:

Dus $32760$ is het enige bovengemiddeld interessant getal kleiner dan $10^{10}$.

(Extra weetje: een meer geoptimaliseerd java-programma leert ons dat dit ook het enige bovengemiddeld interessant getal kleiner $10^{18}$)

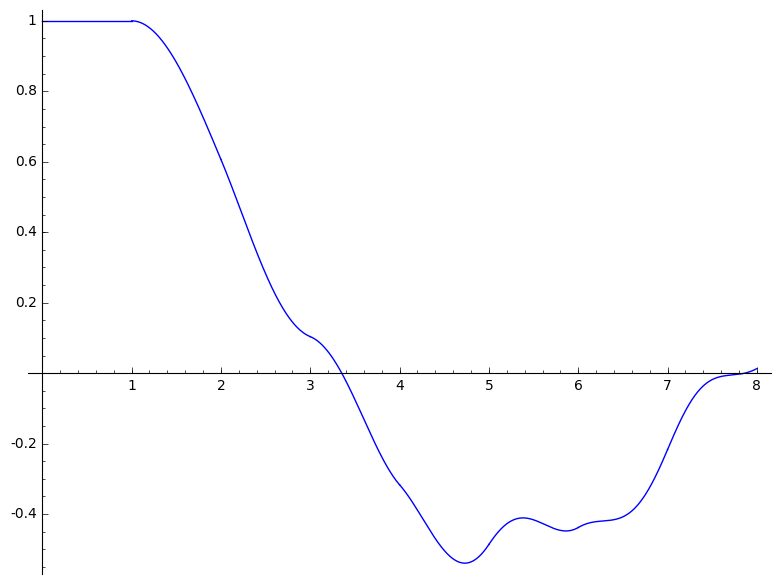
4  Wat een mooie functie!

We zijn op zoek naar een functie $y: \mathbb{R}_{\geq 0} \to \mathbb{R}$ waarvoor het volgende geldt:

• $y(x)$ is continu
• $y(x) = 1$ voor $0 \leq x \leq 1$
• $y^{(R)}(x) = -y(x)s(x) + y^{(L)}(x-2 s(x))$ voor $1 \leq x$
• • met $s(x) = x - \lfloor x\rfloor$
  • met $y^{(R)}(x)$ de rechterafgeleide van $y$ in $x$
  • met $y^{(L)}(x)$ de linkerafgeleide van $y$ in $x$

Hoeveel is $y(5)$ (afgerond tot op 4 cijfers na de komma nauwkeurig)?

De oplossing bestaat erin de functie stuksgewijs te beschouwen.  De vergelijking gebruikt voor waarden in $[n,n+1]$ enkel functiewaarden uit $[n-1,n]$.

Zeg nu zelf, wat een mooie functie!