Inleiding (Numerieke) Analyse in Sage
Symbolisch rekenen
var("x, y")
art = exp(1/(1+x^2))/(1+y^2)*(1/x^2 + 3/y^3)+x
art_plot = implicit_plot(art == 4, (x, -4, 4), (y, -4, 4))
art_plot.show()
art
x + (1/x^2 + 3/y^3)*e^(1/(x^2 + 1))/(y^2 + 1) x + (1/x^2 + 3/y^3)*e^(1/(x^2 + 1))/(y^2 + 1) 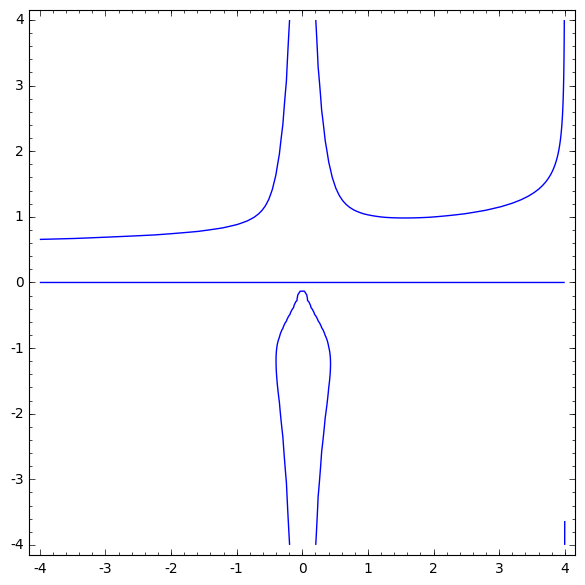
|
nice_plot = art_plot
for y0 in [-.8,-1..-3]:
art_point = (find_root(art(y=y0)-4, -2, -.1), y0)
print art_point
nice_plot += point(art_point, color="red")
nice_plot
(-0.33788948043637007, -0.800000000000000) (-0.3870029905047995, -1.00000000000000) (-0.39943523857520247, -1.20000000000000) (-0.3906906092695037, -1.40000000000000) (-0.3726358466847202, -1.60000000000000) (-0.3515548349816437, -1.80000000000000) (-0.33034158206351877, -2.00000000000000) (-0.3102133576683931, -2.20000000000000) (-0.29160905682373867, -2.40000000000000) (-0.2746166380255696, -2.60000000000000) (-0.2591720909304286, -2.80000000000000) (-0.24515183627871762, -3.00000000000000) (-0.33788948043637007, -0.800000000000000) (-0.3870029905047995, -1.00000000000000) (-0.39943523857520247, -1.20000000000000) (-0.3906906092695037, -1.40000000000000) (-0.3726358466847202, -1.60000000000000) (-0.3515548349816437, -1.80000000000000) (-0.33034158206351877, -2.00000000000000) (-0.3102133576683931, -2.20000000000000) (-0.29160905682373867, -2.40000000000000) (-0.2746166380255696, -2.60000000000000) (-0.2591720909304286, -2.80000000000000) (-0.24515183627871762, -3.00000000000000) 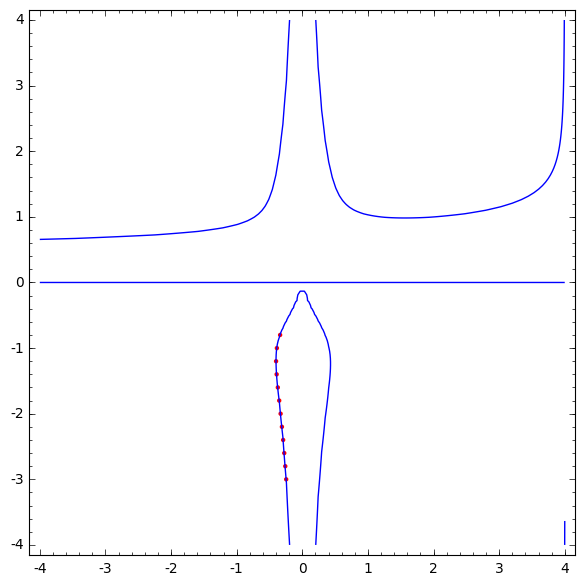
|
Functies
Basis python:
- informatica functies (callables)
- lambda-functies (anonieme functies)
Sage:
- symbolische functies (of expressies)
- onbepaalde functies
var("x")
def f1(x):
return sin(x)^2
f2 = lambda x: sin(x)^2
f3(x) = sin(x)^2
# of f3 = sin(x)^2
f4 = function("f4")(x)
f1 ; f2 ; f3 ; f4
|
|
x0 = 3.0 # in RR, RealField(2048), RDF
f1(x0) ; f2(x0) ; f3(x=x0) ; f4(x=x0)
|
|
parent(f1) ; parent(f2) ; parent(f3) ; parent(f4)
|
|
We berekenen $\frac{d}{dx}f^2$:
diff(f3^2, x); diff(f4^2, x)
|
|
var("y")
diff(f4, y)
|
|
En waarom ook niet $\frac{d^3}{dx dy dx} e^{f(x\sin(y))}$:
dddf3 = diff(e^f3(x=x*sin(y)), x, y, x)
dddf3; dddf3.simplify_full()
|
|
dddf4 = diff(e^f4(x=x*sin(y)), x, y, x)
dddf4; dddf4.simplify_full()
|
|
Integreren
f = sin(x)^2*e^x
plot(f, (x, -3,3))
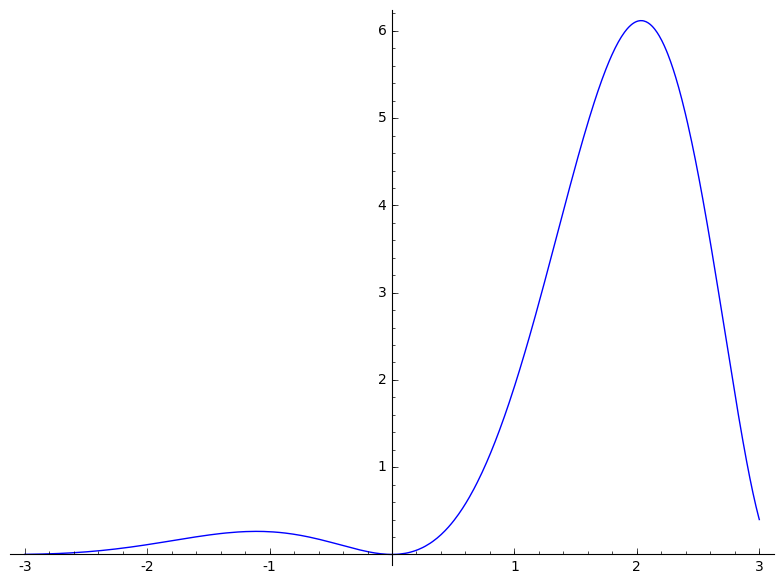
|
F_e = integrate(f, x) # exact
plot(F_e - F_e(x=0), (x, -3, 3)).show()
F_e
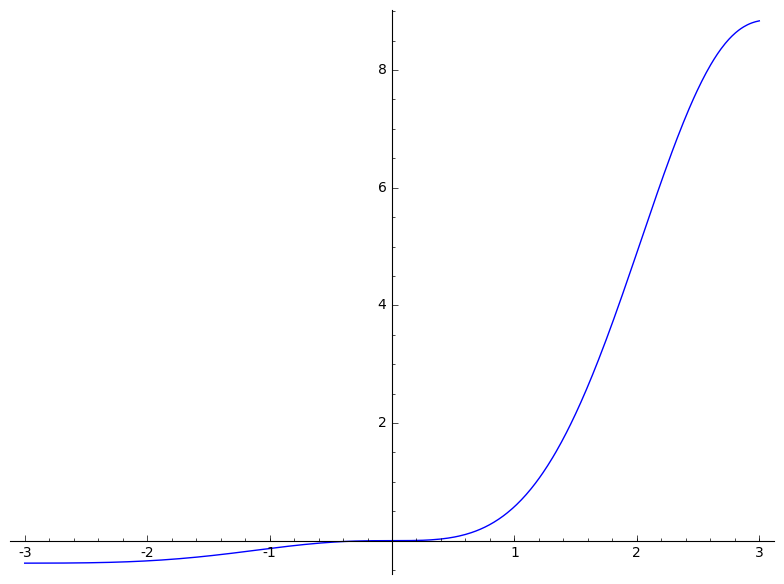
|
integral_numerical(lambda x: f(x=x), 0, 3) # numeriek (antwoord en fout)
|
|
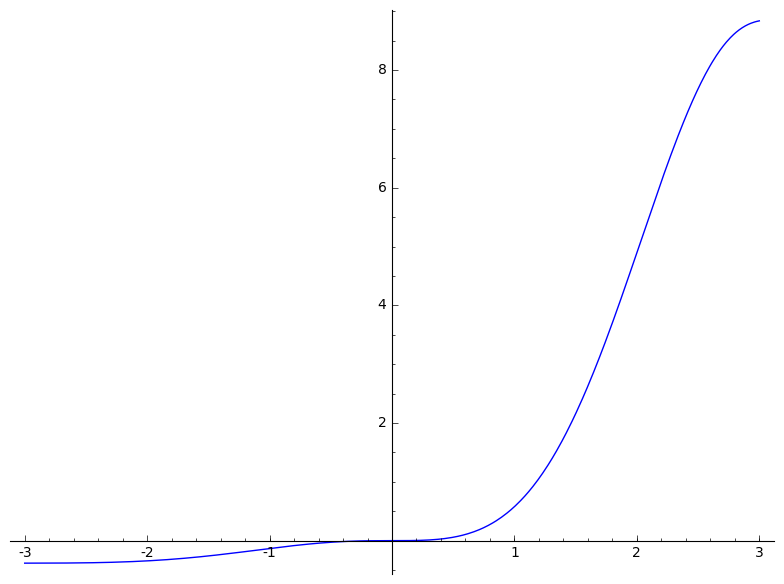
def F_n(x0):
return integral_numerical(lambda x: f(x=x), 0, x0)[0]
plot(F_n, (-3,3))
|
Wanneer welke gebruiken?
- Is er een voorschrift gekend?
- Kan sage ze uitrekenen?
- Hoeveel heb je er nodig?
g = e^cos(x^2)
g
|
|
integrate(g, x, 0, 1)
|
|
numerical_integral(lambda x: g(x=x), 0, 1)
|
|
Extrema's en nulpunten
var("x, y")
f = ( 5000-(x*x+y*y+x*y)/200+25*(x+y)/2 )*exp(-(x*x+y*y)/1000000+3*(x+y)/2000-7/10) # PE 262
f
|
|
plot3d(f, (x, 0, 1600), (y, 0, 1600))
|
|
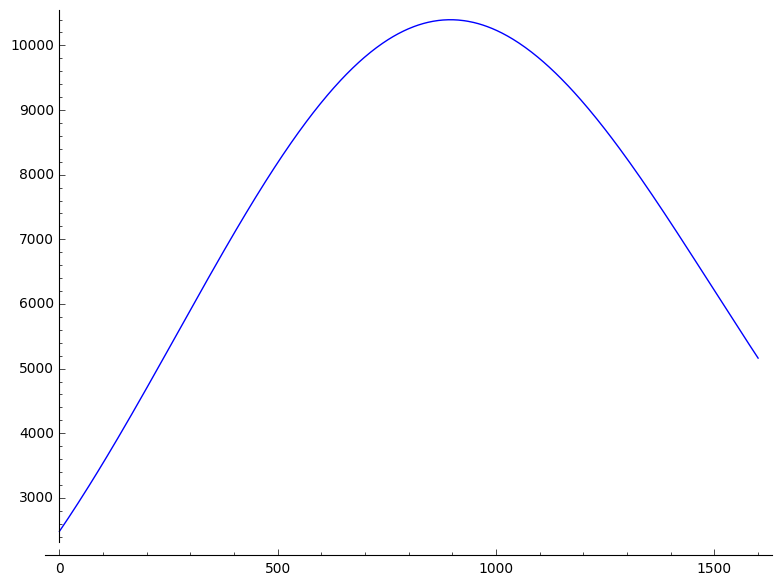
x0 = 0
plot(lambda y: f(x=x0, y=y), (0, 1600))
|
1 dimensie
dfdy = diff(f(x=x0), y)
for sol in solve(dfdy==0, y): # exact
pretty_print(sol.rhs())
pretty_print(sol.rhs().simplify_full())
pretty_print(sol.rhs().simplify_full().n())
print "\n\n"
|
|
find_root(dfdy, 0, 1600) # numeriek
|
|
find_local_maximum(lambda y: f(x=x0, y=y).n(), 0, 1600) # numeriek
|
|
Meer dimensies
for sol in solve([diff(f, x)==0, diff(f, y)==0], x, y, solution_dict=True):
print "f(%.3f, %.3f) = %.3f" % (sol[x], sol[y], f(x=sol[x], y=sol[y])) # exact
f(2766.593, -1016.593) = -2.891 f(-1016.593, 2766.593) = -2.891 f(-417.059, -417.059) = -806.398 f(777.329, 777.329) = 23474.132 f(2056.397, 2056.397) = -353.683 f(2766.593, -1016.593) = -2.891 f(-1016.593, 2766.593) = -2.891 f(-417.059, -417.059) = -806.398 f(777.329, 777.329) = 23474.132 f(2056.397, 2056.397) = -353.683 |
minimize(lambda xy: -f(x=xy[0], y=xy[1]), (800,800)) # numeriek
Optimization terminated successfully.
Current function value: -23474.131917
Iterations: 47
Function evaluations: 89
Optimization terminated successfully.
Current function value: -23474.131917
Iterations: 47
Function evaluations: 89
|
minimize(lambda xy: (diff(f, x)^2 + diff(f, y)^2)(x=xy[0], y=xy[1]), (800, 800)) # numeriek
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 46
Function evaluations: 89
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 46
Function evaluations: 89
|
Gewone differentiaal vergelijkingen (ODE)
We lossen volgende ode op:
$x^{2} \frac{\partial^{2}}{(\partial x)^{2}}g\left(x\right) - x\frac{\partial}{\partial x}g\left(x\right) = 3 \, g\left(x\right)$
met $g(1) = 1$ en $g(5) = 1$
g = function("g")(x)
my_ode = x^2 * diff(g, x, x) - x * diff(g, x) == 3*g
my_ode
|
|
g_e = desolve(my_ode, g) # exact
g_e; plot(g_e, (x, 1, 5))
Traceback (click to the left of this block for traceback) ... ValueError: Variable '_K2' not found
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "_sage_input_15.py", line 10, in <module>
exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("Z19lID0gZGVzb2x2ZShteV9vZGUsIGcpICMgZXhhY3QKZ19lOyBwbG90KGdfZSwgKHgsIDEsIDUpKQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
File "", line 1, in <module>
File "/var/sage/tmpXwql3w/___code___.py", line 4, in <module>
exec compile(u'g_e; plot(g_e, (x, _sage_const_1 , _sage_const_5 ))
File "", line 1, in <module>
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/misc/decorators.py", line 554, in wrapper
return func(*args, **options)
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/plot/plot.py", line 1921, in plot
G = funcs.plot(*args, **original_opts)
File "sage/symbolic/expression.pyx", line 11335, in sage.symbolic.expression.Expression.plot (/opt/sage/sage-7.4/src/build/cythonized/sage/symbolic/expression.cpp:59135)
File "sage/symbolic/expression.pyx", line 11381, in sage.symbolic.expression.Expression._plot_fast_callable (/opt/sage/sage-7.4/src/build/cythonized/sage/symbolic/expression.cpp:59564)
File "sage/ext/fast_callable.pyx", line 456, in sage.ext.fast_callable.fast_callable (/opt/sage/sage-7.4/src/build/cythonized/sage/ext/fast_callable.c:4242)
File "sage/symbolic/expression.pyx", line 11218, in sage.symbolic.expression.Expression._fast_callable_ (/opt/sage/sage-7.4/src/build/cythonized/sage/symbolic/expression.cpp:58356)
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 1580, in fast_callable
return FastCallableConverter(ex, etb)()
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 219, in __call__
return self.arithmetic(ex, operator)
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 1508, in arithmetic
return reduce(lambda x,y: self.etb.call(operator, x,y), operands)
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 1508, in <lambda>
return reduce(lambda x,y: self.etb.call(operator, x,y), operands)
File "sage/ext/fast_callable.pyx", line 734, in sage.ext.fast_callable.ExpressionTreeBuilder.call (/opt/sage/sage-7.4/src/build/cythonized/sage/ext/fast_callable.c:6591)
File "sage/ext/fast_callable.pyx", line 609, in sage.ext.fast_callable.ExpressionTreeBuilder.__call__ (/opt/sage/sage-7.4/src/build/cythonized/sage/ext/fast_callable.c:5685)
File "sage/symbolic/expression.pyx", line 11218, in sage.symbolic.expression.Expression._fast_callable_ (/opt/sage/sage-7.4/src/build/cythonized/sage/symbolic/expression.cpp:58356)
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 1580, in fast_callable
return FastCallableConverter(ex, etb)()
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 218, in __call__
return self.arithmetic(div, div.operator())
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 1508, in arithmetic
return reduce(lambda x,y: self.etb.call(operator, x,y), operands)
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 1508, in <lambda>
return reduce(lambda x,y: self.etb.call(operator, x,y), operands)
File "sage/ext/fast_callable.pyx", line 734, in sage.ext.fast_callable.ExpressionTreeBuilder.call (/opt/sage/sage-7.4/src/build/cythonized/sage/ext/fast_callable.c:6591)
File "sage/ext/fast_callable.pyx", line 609, in sage.ext.fast_callable.ExpressionTreeBuilder.__call__ (/opt/sage/sage-7.4/src/build/cythonized/sage/ext/fast_callable.c:5685)
File "sage/symbolic/expression.pyx", line 11218, in sage.symbolic.expression.Expression._fast_callable_ (/opt/sage/sage-7.4/src/build/cythonized/sage/symbolic/expression.cpp:58356)
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 1580, in fast_callable
return FastCallableConverter(ex, etb)()
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 213, in __call__
return self.symbol(ex)
File "/opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/symbolic/expression_conversions.py", line 1529, in symbol
return self.etb.var(SR(ex))
File "sage/ext/fast_callable.pyx", line 681, in sage.ext.fast_callable.ExpressionTreeBuilder.var (/opt/sage/sage-7.4/src/build/cythonized/sage/ext/fast_callable.c:6190)
ValueError: Variable '_K2' not found
|
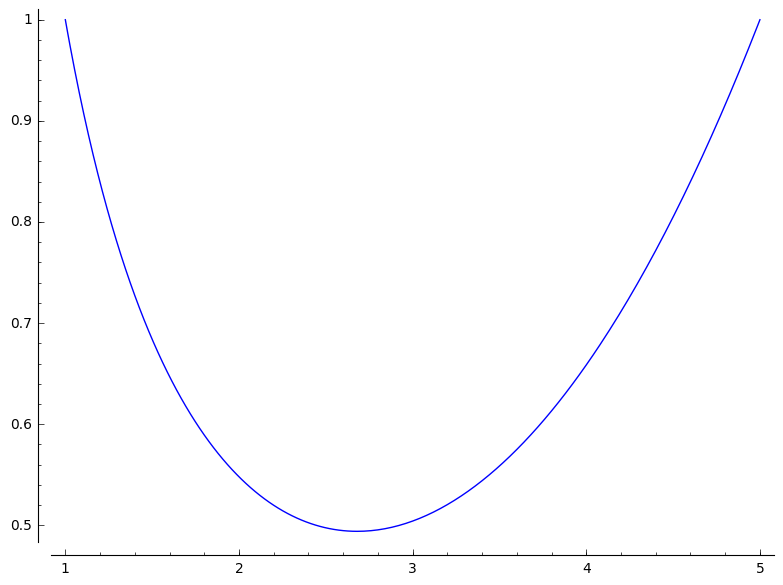
solver = ode_solver()
solver.function = lambda x,y: [y[1], (3*y[0]+x*y[1])/x^2]
solver.y_0 = [1, -38/39]
solver.ode_solve(t_span=[1,5], num_points=300)
solver.plot_solution(interpolate=True)
|
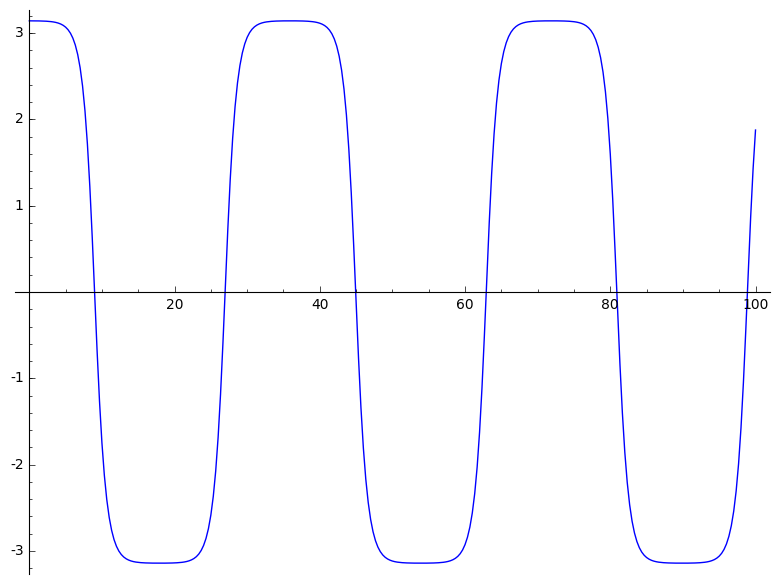
Numeriek kunnen we het pendulum beschrijven zonder dat $\sin(x)$ gelijk moet zijn aan $x$.
$y'' = \sin(y)$
of in de vorm van een eerste orde stelsel: $y0' = y1 \text{ en } y1' = \sin(y0)$
solver = ode_solver()
solver.function = lambda t,y: [y[1], -sin(y[0])]
solver.y_0 = [pi-0.001, 0]
solver.ode_solve(t_span=[0,100], num_points=300)
solver.plot_solution(interpolate=True)
|
|
|
|
|
Een paar problemen:
CoMa:
- 2016 vraag 5
- 2011 vraag 3
- 2011 vraag 5
Project Euler (projecteuler.net)
- 613
- 363
- 525
- 262
- 532
|
|