[ModSim] H3

2015 days ago by Toon.Baeyens

Verdelingen genereren

1.

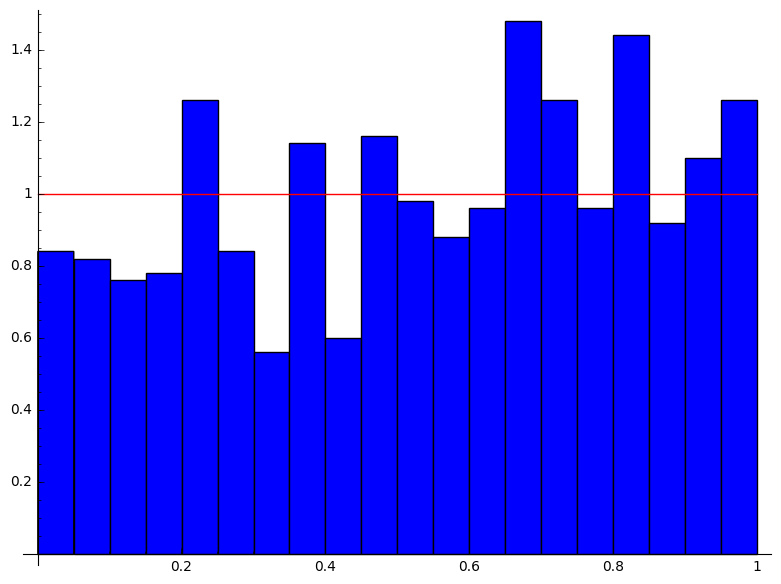
Genereer de exponentiële verdeling vanuit een uniforme verdeling. Basseer je hiervoor op slide 16.

De exponentiele verdeling heeft de volgende vorm:

$$\Phi(x) = \lambda e^{-\lambda x}$$
random() # uniform verdeeld 
        
0.607914174611459
0.607914174611459
uniform = [random() for i in range(1000)] uniform_density = lambda x: 1 if 0 <= x <= 1 else 0 histogram(uniform, bins=20, normed=True) + plot(uniform_density, (0,1), color="red") 
       

2.

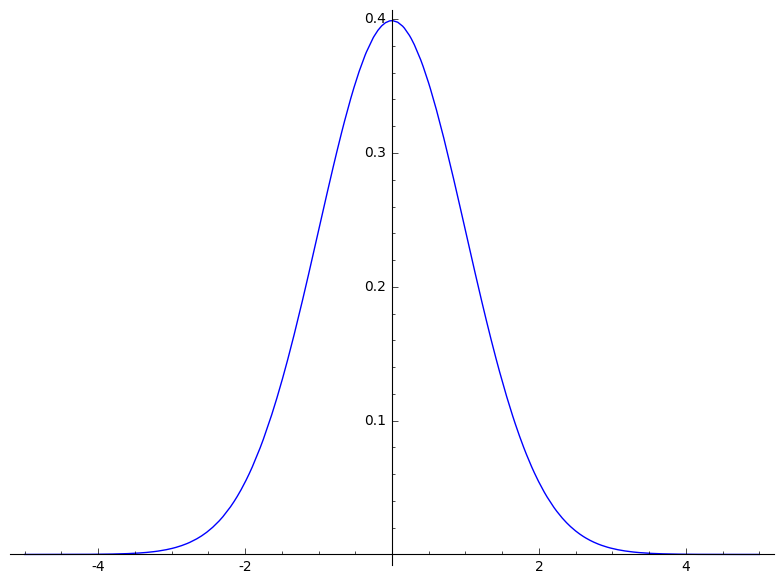
Gebruik https://en.wikipedia.org/wiki/Box%E2%80%93Muller_transform om vanuit 2 uniforme verdelingen 2 normale verdelingen te verkrijgen.

Meer informatie over de normale distributie is te vinden op: https://en.wikipedia.org/wiki/Normal_distribution.
mu = 0 sigma = 1 normal_density = 1/sqrt(2*pi*sigma^2) * exp(-(x-mu)^2/(2*sigma^2)) plot(normal_density, (x, -5,5)) 
       
 
       

3.

(Examen 2017-2018)

Simuleer een binomiaal verdeelde veranderlijke ($\textsf{Bin}(n, p)$) met $n = 12$ en $p = 0.25$ door volledig te steunen op de uniforme verdeling.

Simuleer deze veranderlijke vervolgens 10000 keer een maak een histogram om de verdeling weer te geven.
Bereken eveneens het steekproefgemiddelde ($\bar{x}$).
 
       

Monte Carlo methoden

4.

Implementeer de Monte Carlo methode om kwadraturen te berekenen. 

$$ \int_a^b f(x) \, d x \approx \frac{b-a}{n} \sum_{k=1}^{n} f(x_k)$$

met $n$ het aantal willekeurig gekozen punten $x_k$.

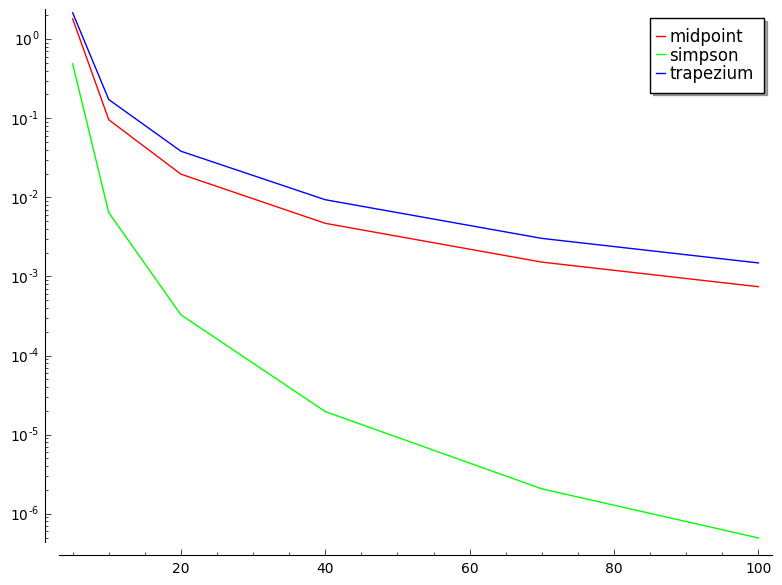
Je kan de reeds gegeven code gebruiken om de mote_carlo methode te vergelijken met andere kwadratuur formules.

Probeer zeker eens een paar verschillende functies en verschillende stappen en aantal punten uit. Experimenteer!
def plot_errors(errors, steps): """ errors = [{'rule1': error_rule_1, ...} for _ in steps] """ colors = rainbow(len(errors[0])) g = Graphics() for color, line in zip(colors, zip(*map(lambda d: d.items(), errors))): g += list_plot_semilogy(zip(steps, zip(*line)[1]), plotjoined=True, color=color, legend_label=line[0][0]) return g def middelpunt(f, a, b): return f((a+b)/2)*(b-a) def trapezium(f, a, b): return (f(a)+f(b))*(b-a)/2 def simpson(f, a, b): return 2./3*middelpunt(f,a,b) + 1./3*trapezium(f, a ,b) def integrate(f, a, b, steps, rule=trapezium): total = 0 h = (b-a)/steps for i in range(steps): x0 = RDF(a+h*i) x1 = RDF(x0+h) total += RDF(rule(f, x0, x1)) return total 
       
f = lambda x: sin(9*x) 
       
real_value = numerical_integral(f, 0, pi)[0] all_steps = [5,10,20,40,70,100] errors = [{ 'trapezium': abs(integrate(f, 0, pi, rule=trapezium, steps=steps) - real_value), 'midpoint': abs(integrate(f, 0, pi, rule=middelpunt, steps=steps) - real_value), 'simpson': abs(integrate(f, 0, pi, rule=simpson, steps=steps) - real_value) } for steps in all_steps] plot_errors(errors, steps=all_steps) 
       

5.

(Project 2017 - 2018)

De Haltonsequentie is een quasi-random number generator, zie https://en.wikipedia.org/wiki/Halton_sequence#Implementation_in_pseudocode.

Implementeer het algoritme dat daar gegeven wordt.

Print dan ook de eerste 10 elementen in basis 2 en 3, om je implementatie te controlleren.
def halton(base, index): # TODO return 0 
       

6.

(Project 2017 - 2018)

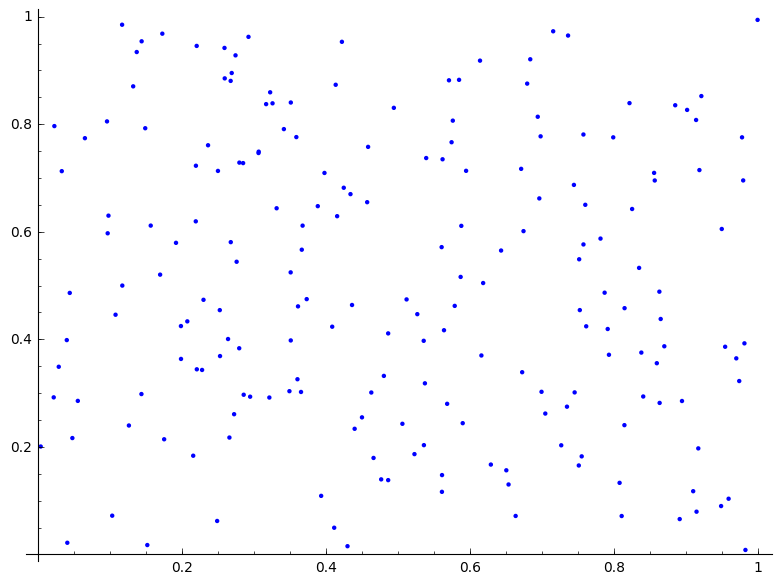
Door $n$ sequenties van de Haltonsequentie te 'zippen', kan men quasi-random punten in $[0,1]^n$ verkrijgen.

Werk in 2 dimensies en vergelijk eens verschillende combinaties basissen (2 en 3, 5 en 13...). Maak voldoende plots.

Vergelijk ook eens de resultaten me uniform gegenereerde punten.
list_plot([(random(), random()) for i in range(200)]) 
       

7.

(Project 2017 - 2018)

Gebruik de Holtonsequentie om via een Monte Carlo methode

$$ \int_0^1 \cdots \int_0^1  \prod_{i=1}^{s} \frac{\pi}{2} \sin(\pi x)\;\mbox{d}x_s \cdots \mbox{d}x_1$$

te berekenen. Het exacte resultaat is voor elke dimensie $s$ $1$.