[ModSim] H3 (oplossingen)

2015 days ago by Toon.Baeyens

Verdelingen genereren

1.

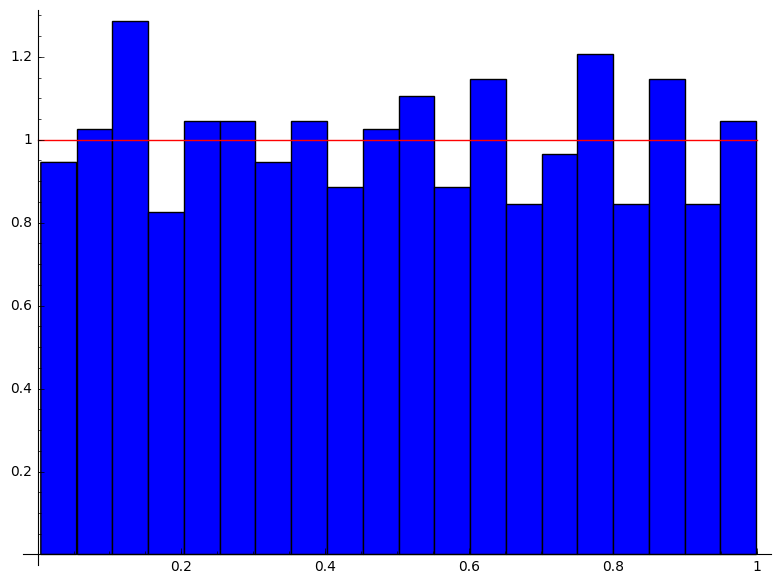
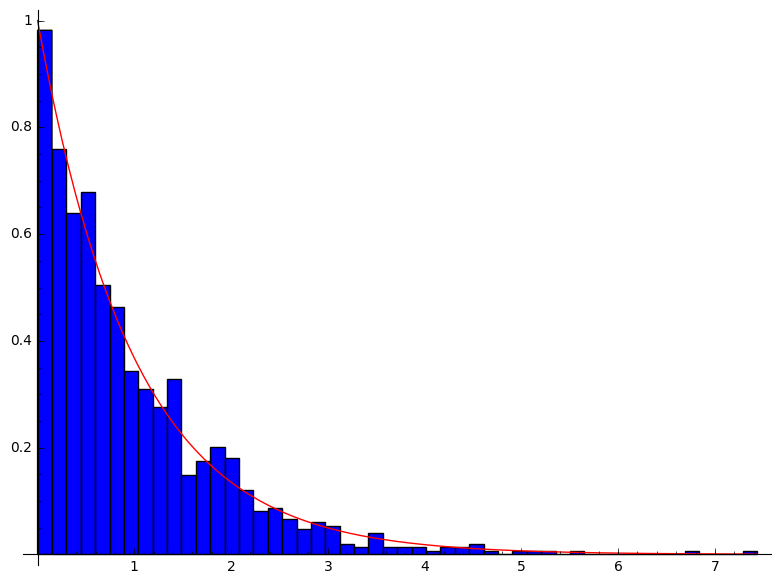
Genereer de exponentiële verdeling vanuit een uniforme verdeling. Basseer je hiervoor op slide 16.

De exponentiele verdeling heeft de volgende vorm:

$$f_\lambda(x) = \lambda e^{-\lambda x}$$
random() # uniform verdeeld 
        
0.27019886209206534
0.27019886209206534
uniform = [random() for i in range(1000)] uniform_density = lambda x: 1 if 0 <= x <= 1 else 0 histogram(uniform, bins=20, normed=True) + plot(uniform_density, (0,1), color="red") 
       
def sample_exp(lamb=1): return -ln(1-random())/lamb 
       
lamb = 1 exp_distribution = [sample_exp(lamb=lamb) for i in range(1000)] exp_distribution_density = lambda x: lamb*exp(-lamb*x) histogram(exp_distribution, bins=50, normed=True) + plot(exp_distribution_density, (0,max(exp_distribution)), color="red") 
       

2.

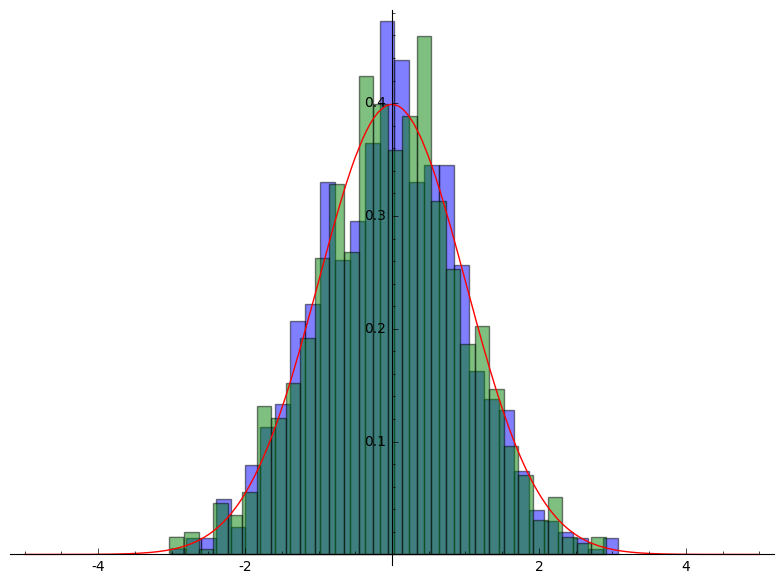
Gebruik https://en.wikipedia.org/wiki/Box%E2%80%93Muller_transform om vanuit 2 uniforme verdelingen 2 normale verdelingen te verkrijgen.

Meer informatie over de normale distributie is te vinden op: https://en.wikipedia.org/wiki/Normal_distribution.
mu = 0 sigma = 1 normal_density = 1/sqrt(2*pi*sigma^2) * exp(-(x-mu)^2/(2*sigma^2)) 
       
def sample_2_normals(): R = sqrt(-2*ln(random())) theta = 2*pi*random() return R*cos(theta), R*sin(theta) 
       
Z0 , Z1 = zip(*[sample_2_normals() for i in range(1000)]) g = histogram(Z0, color="blue", normed=True, alpha=.5, bins=30) g += histogram(Z1, color="green", normed=True, alpha=.5, bins=30) g += plot(normal_density, (x, -5,5), color="red") g 
       

3.

(Examen 2017-2018)

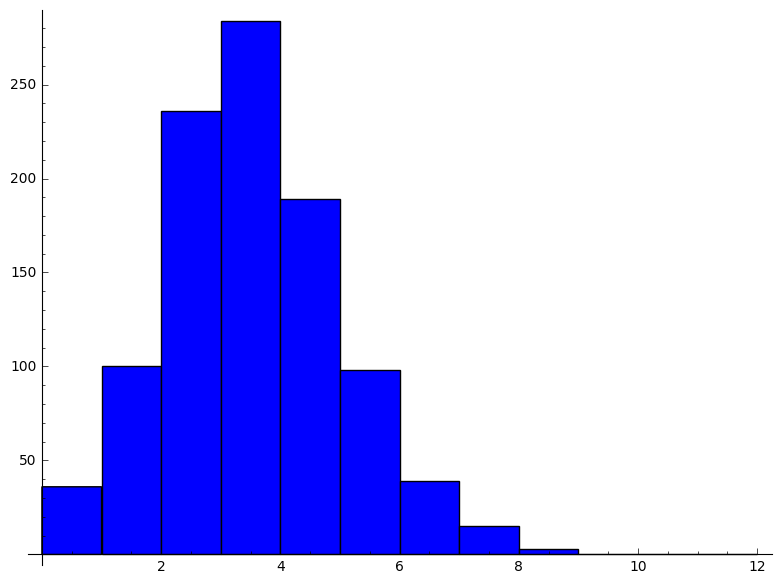
Simuleer een binomiaal verdeelde veranderlijke ($\textsf{Bin}(n, p)$) met $n = 12$ en $p = 0.25$ door volledig te steunen op de uniforme verdeling.

Simuleer deze veranderlijke vervolgens 10000 keer een maak een histogram om de verdeling weer te geven.
Bereken eveneens het steekproefgemiddelde ($\bar{x}$).
n = 12 p = .25 samples = [sum(random() < p for i in range(n)) for j in range(1000)] histogram(samples, range=(0,12), bins = 12) 
       
rand 
        
3.03300000000000
3.03300000000000

Monte Carlo methoden

4.

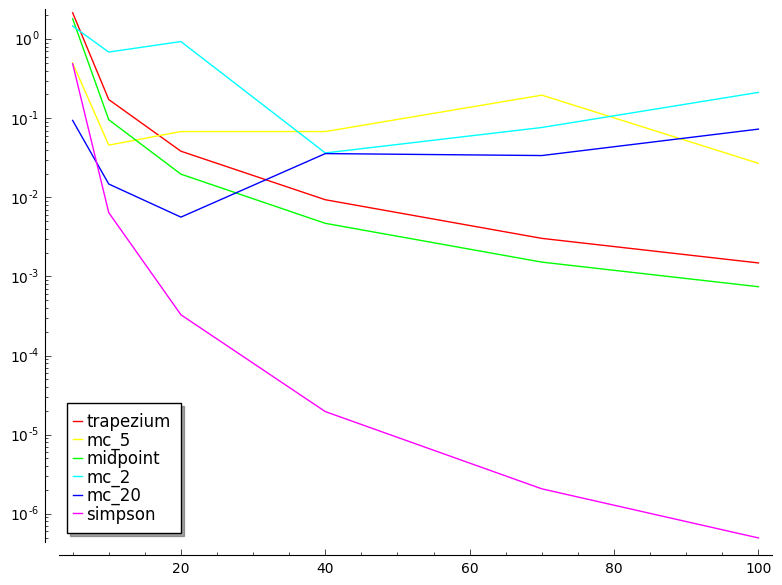
Implementeer de Monte Carlo methode om kwadraturen te berekenen. 

$$ \int_a^b f(x) \, d x \approx \frac{b-a}{n} \sum_{k=1}^{n} f(x_k)$$

met $n$ het aantal willekeurig gekozen punten $x_k$.

Je kan de reeds gegeven code gebruiken om de mote_carlo methode te vergelijken met andere kwadratuur formules.

Probeer zeker eens een paar verschillende functies en verschillende stappen en aantal punten uit. Experimenteer!
def plot_errors(errors, steps): """ errors = [{'rule1': error_rule_1, ...} for _ in steps] """ colors = rainbow(len(errors[0])) g = Graphics() for color, line in zip(colors, zip(*map(lambda d: d.items(), errors))): g += list_plot_semilogy(zip(steps, zip(*line)[1]), plotjoined=True, color=color, legend_label=line[0][0]) return g def middelpunt(f, a, b): return f((a+b)/2)*(b-a) def trapezium(f, a, b): return (f(a)+f(b))*(b-a)/2 def simpson(f, a, b): return 2./3*middelpunt(f,a,b) + 1./3*trapezium(f, a ,b) def integrate(f, a, b, steps, rule=trapezium): total = 0 h = (b-a)/steps for i in range(steps): x0 = RDF(a+h*i) x1 = RDF(x0+h) total += RDF(rule(f, x0, x1)) return total 
       
def monte_carlo(f, a, b, points=10): total = 0 for i in range(points): total += RDF((b-a)*f(a + (b-a)*random())) total /= points return total 
       
f = lambda x: sin(9*x) 
       
real_value = numerical_integral(f, 0, pi)[0] all_steps = [5,10,20,40,70,100] errors = [{ 'trapezium': abs(integrate(f, 0, pi, rule=trapezium, steps=steps) - real_value), 'midpoint': abs(integrate(f, 0, pi, rule=middelpunt, steps=steps) - real_value), 'simpson': abs(integrate(f, 0, pi, rule=simpson, steps=steps) - real_value), 'mc_20': abs(monte_carlo(f, 0, pi, points=20*steps)-real_value), 'mc_2': abs(monte_carlo(f, 0, pi, points=2*steps)-real_value), 'mc_5': abs(monte_carlo(f, 0, pi, points=5*steps)-real_value) } for steps in all_steps] plot_errors(errors, steps=all_steps) 
       

5.

(Project 2017 - 2018)

De Haltonsequentie is een quasi-random number generator, zie https://en.wikipedia.org/wiki/Halton_sequence#Implementation_in_pseudocode.

Implementeer het algoritme dat daar gegeven wordt.

Print dan ook de eerste 10 elementen in basis 2 en 3, om je implementatie te controlleren.
def halton(base, index): f = 1 r = 0 while index > 0: f = f / base r += f*(index%base) index = floor(index/base) return r 
       
[halton(2, i) for i in range(1, 10)] 
        
[1/2, 1/4, 3/4, 1/8, 5/8, 3/8, 7/8, 1/16, 9/16]
[1/2, 1/4, 3/4, 1/8, 5/8, 3/8, 7/8, 1/16, 9/16]
[halton(3, i) for i in range(1, 10)] 
        
[1/3, 2/3, 1/9, 4/9, 7/9, 2/9, 5/9, 8/9, 1/27]
[1/3, 2/3, 1/9, 4/9, 7/9, 2/9, 5/9, 8/9, 1/27]

6.

(Project 2017 - 2018)

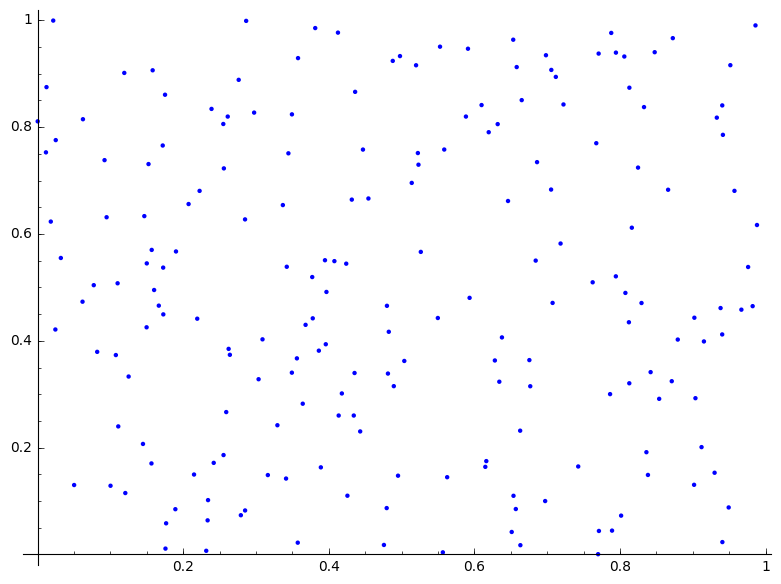
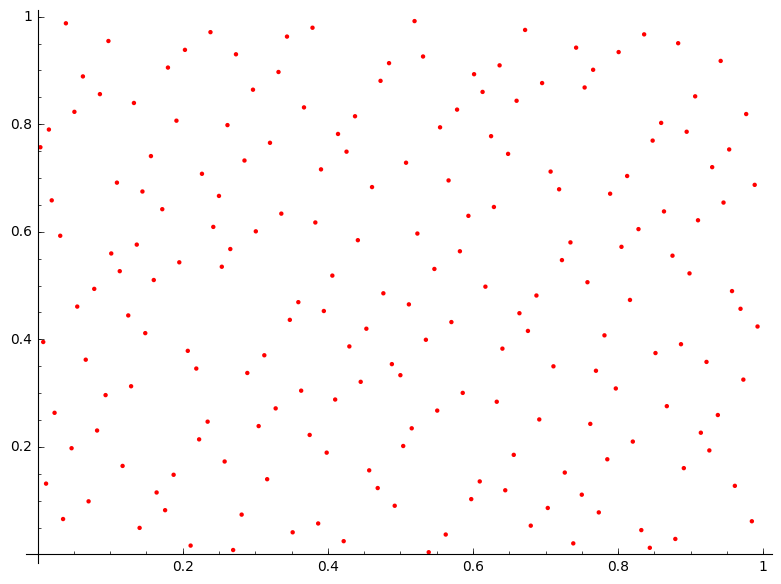
Door $n$ sequenties van de Haltonsequentie te 'zippen', kan men quasi-random punten in $[0,1]^n$ verkrijgen.

Werk in 2 dimensies en vergelijk eens verschillende combinaties basissen (2 en 3, 5 en 13...). Maak voldoende plots.

Vergelijk ook eens de resultaten me uniform gegenereerde punten.
list_plot([(random(), random()) for i in range(200)]).show() list_plot([(halton(2, i), halton(3, i)) for i in range(1,200)], color="red") 
       

list_plot([(halton(2, i), halton(3, i)) for i in range(1,20)], color="red").show() list_plot([(halton(11, i), halton(7, i)) for i in range(1,20)], color="red").show() 
       

7.

(Project 2017 - 2018)

Gebruik de Holtonsequentie om via een Monte Carlo methode

$$ \int_0^1 \cdots \int_0^1  \prod_{i=1}^{s} \frac{\pi}{2} \sin(\pi x)\;\mbox{d}x_s \cdots \mbox{d}x_1$$

te berekenen. Het exacte resultaat is voor elke dimensie $s$ $1$.