Differentiaalvergelijkingen
Om differentiaalvergelijkingen numeriek op te lossen kan men gebruik maken van:
def ode(f, t0, t1, y0, algorithm="rkf45", **kwargs):
"""
Solve y' = f(t, y) * y between t0 and t1, with y(t0) = y0.
At each step with size h use the function step.
"""
d1 = y0 in RR
if d1:
y0 = [y0]
import collections
solver = ode_solver()
solver.function = f
solver.t_span = [t0] + (t1 if isinstance(arg, collections.Iterable) else [t1])
solver.y_0 = y0
solver.algorithm = algorithm
solver.error_rel=1e-9
solver.ode_solve(**kwargs)
t, y = zip(*solver.solution)
if d1:
y = map(lambda u: u[0], y)
return t, y
|
|
f0 = lambda t, (y,): [y]
t, y = ode(f0, 0.,3., 1., num_points=100)
list_plot(zip(t, y), plotjoined=True)
|
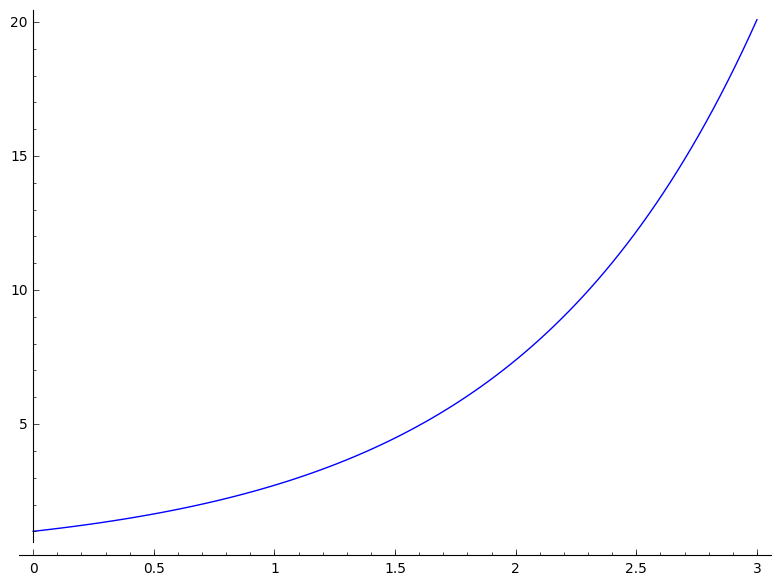
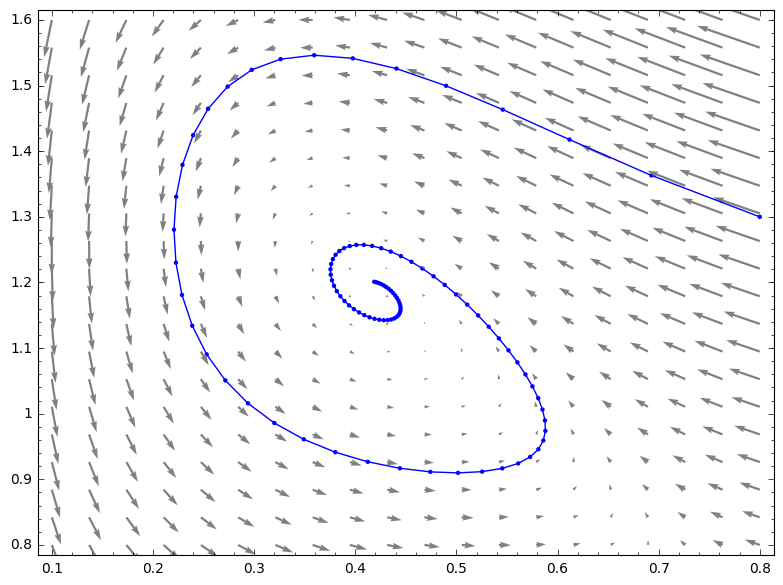
Het gebruik van deze functie illustreren we met behulp van het probleem:
| $x =$ | $2 x (1-x) - \frac{x y}{x + 0.6}$ |
| $y =$ | $-\frac{y}{4} + \frac{x y}{x + 0.6} - \frac{{y^2}^{\phantom{1}}}{5 (y^2 + \frac{1}{16})}$ |
fx = lambda x, y: 2.*x*(1.-x)-x*y/(x+0.6)
fy = lambda x, y: -y/4. + x*y/(x+.6)-y*y/(5.*(y*y+1./16.))
f = lambda t, (x, y): [fx(x, y), fy(x, y)]
|
|
t, results = ode(f, t0=0, t1=30, y0=[.8,1.3], num_points=100)
g = list_plot(results, plotjoined=True)
g += list_plot(results)
g += plot_vector_field((fx, fy), (.1,.8), (.8,1.6), color="gray")
g.show()
|
Experimenteer met de gegeven code:
- Kies andere beginvoorwaarden
- Plot verschillende banen
- ...
|
|
Numerieke methoden
Implementeer de stapmethode voor de voorwaartse Euler.
def forwardEuler(f, t0, y0, h, **kwargs):
"""
One step in the problem y' = f(t, y) * y. From t0 to t0 + h.
"""
dy = f(t0, y0)
return y0 + dy*h
|
|
Test met behulp van stepper jouw implementatie voor het probleem:
$$ y' = \lambda y $$
met $y(0) = 1$.
Vergelijk verschillende staplengtes met de exacte oplossing $y = e^{\lambda t}$.
def vectorize(arg):
"""
Makes from on object that is vectorlike (a vector or a number).
>>> vectorize(3)
3
>>> vectorize([1,2])
vector([1,2])
"""
if arg in RR:
return RDF(arg)
elif arg[0] in RR:
return vector(RDF, arg)
else:
return matrix(RDF, arg)
def stepper(f, t0, t1, y0, h, step=forwardEuler, name=None, verbose=False, statistics=False, jacobian=None, **kwargs):
"""
Solve y' = f(t, y) * y between t0 and t1, with y(t0) = y0.
At each step with size h use the function step.
>>> t, y = stepper(lambda t, y: y, t0=0, t1=1, y0=1, h=.5)
>>> t
[0, 0.5, 1.0]
>>> y
[1, 1.5, 2.25]
"""
stats = {'count': 0, 'Jcount': 0, 'name': name if name else 'ode-%d'%(randint(10, 100))}
def F(*args):
stats['count'] += 1
return vectorize(f(*args))
def J(*args):
stats['Jcount'] += 1
return vectorize(jacobian(*args))
if jacobian:
kwargs['jacobian'] = J
t = [vectorize(t0)]
y = [vectorize(y0)]
while t[-1] < t1:
y.append(step(F, t[-1], y[-1], h, **kwargs))
t.append(t[-1] + h)
if verbose:
print "Statistics of '%s'"%stats['name']
print "| % 5d func-evals"%stats['count']
if statistics:
return t, y, stats
else:
return t, y
|
|
Implementeer nu ook de achterwaartse Euler methode en de trapezium methode.
Merk op dat deze methoden impliciet zijn. Het zal dus nodig zijn om newton raphson toe te passen.
De achterwaartse Euler methode gebruikt het schema $y_{n+1} = y_{n} + h f(t_{n+1}, y_{n+1})$.
De trapezium methode gebruikt het schema $y_{n+1} = y_{n} + (f(t_{n}, y_{n}) + f(t_{n+1}, y_{n+1}))\frac{h}{2}$.
Ter herinnering:
https://en.wikipedia.org/wiki/Newton%27s_method
https://en.wikipedia.org/wiki/Newton%27s_method#k_variables,_k_functions
def identity(y):
if y in RR:
return 1
else:
return matrix.identity(len(y))
def newtonRaphson(y0, f, jacobian, max_iter=20, error=1e-5):
y = y0
for _ in range(max_iter):
fy = f(y)
if abs(fy) < error:
break
if y in RR:
y -= fy/jacobian(y)
else:
y -= jacobian(y).solve_right(fy)
else:
print("Newton-Raphson did not converge")
return y
def backwardEuler(f, t0, y0, h, jacobian):
"""
The jacobian is given for a 2 dimensional problem as:
lambda t, (x, y): [[x_dx, x_dy], [y_dx, y_dy]]
"""
t1 = t0 + h
Fy = lambda y: y0 + f(t1, y)*h - y
dFy = lambda y: jacobian(t1, y)*h - identity(y)
return newtonRaphson(y0, Fy, dFy)
def trapezoid(f, t0, y0, h, jacobian):
t1 = t0 + h
f0 = f(t0, y0)
Fy = lambda y: y0 + (f0 + f(t1, y))*h/2 - y
dFy = lambda y: jacobian(t1, y)*h/2 - identity(y)
return newtonRaphson(y0, Fy, dFy)
|
|
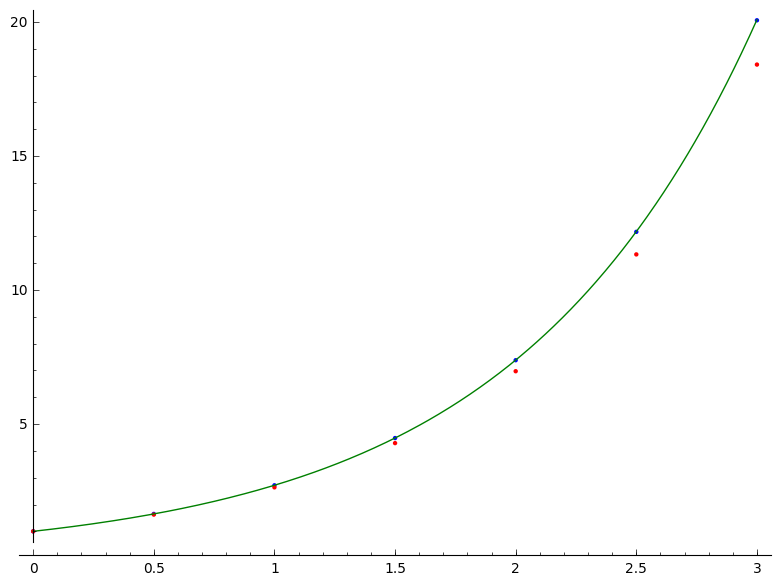
Test jouw implementatie van deze impliciete methoden ten opzichte van $y' = \lambda y$ en $y(0) = 1$ over het interval $t \in [0,3]$. Maak ook een tabel die voor elke van de drie methoden de globale fout uitdrukt in functie van de stapgrootte. (Kies $\lambda < 1.5$)
Vergelijk de staplengtes $2^{-1}$, $2^{-2}$, ..., $2^{-8}$ en bekijk ook eens $\log_2$ van de globale fout.
l = 1
f = lambda t, y: l*y
t0 = 0.
t1 = 3.
y0 = 1.
hs = [2.^-i for i in [1..7]]
args = [f, t0, t1, y0]
exact = ode(*args)[-1][-1]
results = [[stepper(*args, h=h, step=step, jacobian=lambda t, y: l, verbose=False, statistics=True) for h in hs]
for step in [forwardEuler, backwardEuler, trapezoid]]
header_row = [["stepsize"]+["%f, (#f, #J)"%h for h in hs]]
pretty_print(LatexExpr(r"\text{error}"))
show(table(header_row+
[[name] + ["%f (%d, %d)"%((y[-1]-exact), stats['count'], stats['Jcount']) for t, y, stats in method]
for name, method in zip(["forward", "backward", "trapezoid"], results)],
header_row=True, header_column=True
))
print "\n"
pretty_print(LatexExpr(r"\log_2(|\text{error}|)"))
show(table(header_row+
[[name] + ["%f (%d)"%(log(abs(y[-1]-exact))/log(2), stats['count']) for t, y, stats in method]
for name, method in zip(["forward", "backward", "trapezoid"], results)],
header_row=True, header_column=True
))
|
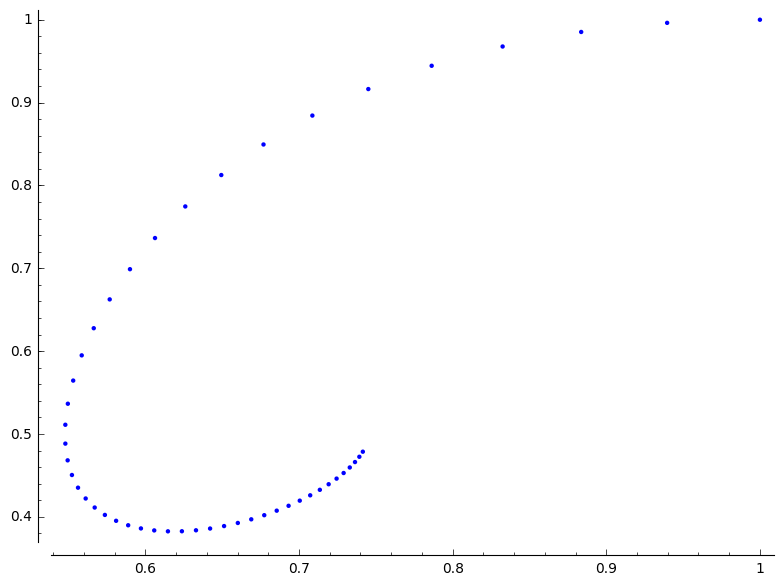
Test al deze methoden ook tegenover
$$x' = -2yx+x\\y'=x-y/x$$
met $x(0) = y(0) = 1$. Bekijk verschillende stapgroottes.
l = 1
f = lambda t, (x, y): [-2*x*y+x, x-y/x]
t0 = 0.
t1 = 3.
y0 = [1.,1.]
jacobian=lambda t, (x, y): [[-2*y+1, -2*x],[1+y/x^2, -1/x]]
hs = [2.^-i for i in [1..7]]
args = [f, t0, t1, y0]
exact = vectorize(ode(*args)[-1][-1])
results = [[stepper(*args, h=h, step=step, jacobian=jacobian, verbose=False, statistics=True) for h in hs]
for step in [forwardEuler, backwardEuler, trapezoid]]
header_row = [["stepsize"]+["%f, (#f, #J)"%h for h in hs]]
pretty_print(LatexExpr(r"\text{error}"))
show(table(header_row+
[[name] + ["%f (%d, %d)"%(abs(y[-1]-exact), stats['count'], stats['Jcount']) for t, y, stats in method]
for name, method in zip(["forward", "backward", "trapezoid"], results)],
header_row=True, header_column=True
))
print "\n"
pretty_print(LatexExpr(r"\log_2(|\text{error}|)"))
show(table(header_row+
[[name] + ["%f (%d)"%(log(abs(y[-1]-exact))/log(2), stats['count']) for t, y, stats in method]
for name, method in zip(["forward", "backward", "trapezoid"], results)],
header_row=True, header_column=True
))
|
list_plot(results[2][3][1])
|
En ook eens met het probleem $y'' = -y$ .
|
|
|
|
Runge-Kutta methoden
Deze methode worden gegeven door het volgende schema:
$$y_{k+1} = y_{k} + h \sum_{i=1}^s b_i K_i$$
met $K_i = f(t_k + c_i h, y_k + h\sum_{j=1}^{s} a_{ij} K_j)$.
Zo'n methodes kunnen dus samengevat worden door zijn Butcher-tableau:
| $c_1$ | $a_{11}$ | $a_{12}$ | $\cdots$ | $a_{1s}$ |
| $c_2$ | $a_{21}$ | $a_{22}$ | $\cdots$ | $a_{2s}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $c_s$ | $a_{s1}$ | $a_{s2}$ | $\cdots$ | $a_{ss}$ |
| $b_1$ | $b_2$ | $\cdots$ | $b_s$ |
Men kan zien dat de methode expliciet is als $a_{ij} = 0$ voor alle $j \geq i$.
Implementeer een fuctie die een step-functie teruggeeft volgens het gegeven expliciete tableau.
def runge_kutta_step(s, a, b, c):
"""
>>> runge_kutta_step(1, [[0]], [1], [0])
# De voorwaartse euler
>>> runge_kutta_step(2, [[0, 0], [1, 0]], [.5, .5], [0, 1])
# De methode van Heun
"""
def step(f, t0, y0, h, **kwargs):
K = [f(t0, y0)]
for i in range(1, s):
K.append(f(t0+c[i]*h, y0 + h*sum(a[i][j]*K[j] for j in range(i))))
return y0 + h*sum(K[i]*b[i] for i in range(s))
return step
|
|
Genereer de vergelijkende tabellen (voor beide problemen) hier opnieuw met twee extra rijen voor de methode van Heun en de 'echte' Runge-Kutta methode.
rk_euler = runge_kutta_step(1, [[0]], [1], [0])
rk_heun = runge_kutta_step(2, [[0, 0], [1, 0]], [.5, .5], [0, 1])
rk_echte = runge_kutta_step(4, [[0.,0.,0.,0.],[.5,0.,0.,0.],[0.,.5,0.,0.],[0.,0.,1.,0.]],[1./6, 1./3, 1./3, 1./6], [0.,.5,.5,1.])
|
|
t_e, y_e = stepper(lambda t, y: y, 0.,3.,1., h=.5, step=rk_echte)
t_h, y_h = stepper(lambda t, y: y, 0.,3.,1., h=.5, step=rk_heun)
list_plot(zip(t_e, y_e)) + list_plot(zip(t_h, y_h), color="red") + plot(exp, (0,3), color="green")
|
l = 1
f = lambda t, (x, y): [-2*x*y+x, x-y/x]
t0 = 0.
t1 = 3.
y0 = [1.,1.]
jacobian=lambda t, (x, y): [[-2*y+1, -2*x],[1+y/x^2, -1/x]]
hs = [2.^-i for i in [1..7]]
args = [f, t0, t1, y0]
exact = vectorize(ode(*args)[-1][-1])
results = [[stepper(*args, h=h, step=step, jacobian=jacobian, verbose=False, statistics=True) for h in hs]
for step in [forwardEuler, backwardEuler, trapezoid, rk_heun, rk_echte]]
header_row = [["stepsize"]+["%f, (#f, #J)"%h for h in hs]]
pretty_print(LatexExpr(r"\text{error}"))
show(table(header_row+
[[name] + ["%f (%d, %d)"%(abs(y[-1]-exact), stats['count'], stats['Jcount']) for t, y, stats in method]
for name, method in zip(["forward", "backward", "trapezoid", "heun", "rk"], results)],
header_row=True, header_column=True
))
print "\n"
pretty_print(LatexExpr(r"\log_2(|\text{error}|)"))
show(table(header_row+
[[name] + ["%f (%d)"%(log(abs(y[-1]-exact))/log(2), stats['count']) for t, y, stats in method]
for name, method in zip(["forward", "backward", "trapezoid", "heun", "rk"], results)],
header_row=True, header_column=True
))
|
|
|