Bekijk de golfvergelijking voor een functie $y(t, x)$:
$$\frac{\partial^2 y}{\partial t^2} = c^2\frac{\partial^2 y}{\partial x^2} $$
De volgende code implementeert een semidiscretisatie
|
|
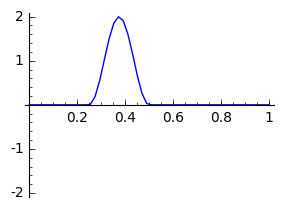
|
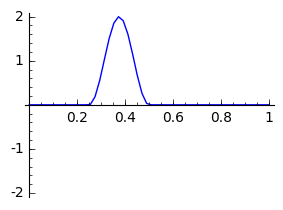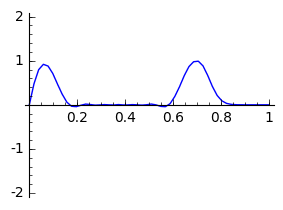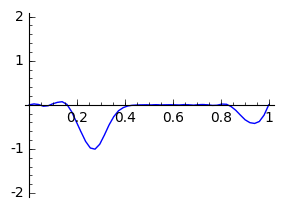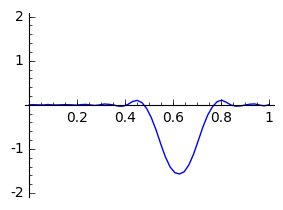
|
- Wijzig eens de beginvoorwaarde zodanig dat er twee pulsen naast elkaar zijn.
- Kan je de nauwkeurigheid verhogen/verlagen? Wat merk je?
- Welke impact heeft $c$?
|
|
|
|
Verander (vereenvoudig) de code die gebruikt werd voor de golfvergelijking om ook de warmtevergelijking aan te pakken:
$$\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2}$$
randvoorwaarden $u(t, 0) = u(t, 1) = 0$ en $u(0, x) = 1$ als $\frac{1}{4} \leq x \leq \frac{3}{4}$ en anders $u(0, x) = 0$. Probeer verschillende tijdsschalen uit.
|
|
|
|
- Welk gedrag vertoont de warmtevergelijking bij $t \to \infty$? Wat is dit bij de golfvergelijking?
- Wat moet je wijzigen om het met randvoorwaarde (u(t,1) = 0.5$ op te lossen?
|
|
|
|
Volledige discretisatie
De schrödingervergelijking
$$ -\frac{\partial^2 u}{\partial x^2}-\frac{\partial^2 u}{\partial x^2} + V(x, y) u = E u $$
is een eigenwaardeprobleem. Stel $V(x, y) = (1+x^2) ( 1 + y^2)$ en $u(-5.5, y) = u(5.5, y) = u(x, -5.5) = u=(x, 5.5) = 0$.
Discretiseer de gezochte functie $u$ in een vector (van lengte $n^2$):
$$ v = (u(x_0, y_0), \dots, u(x_0, y_{n-1}), u(x_1, y_0), \dots, u(x_{n-1}, y_{n-1}))$$
Benader de vergelijking door:
$$ \frac{\partial^2 u}{\partial x^2}(x_i, y_j) = \frac{u(x_{i-1}, y_j) - 2u(x_i, y_j) + u(x_{i+1}, y_j)}{h^2} $$
$$ \frac{\partial^2 u}{\partial y^2}(x_i, y_j) = \frac{u(x_i, y_{j-1}) - 2u(x_i, y_j) + u(x_{i}, y_{j+1})}{h^2} $$
Schrijf nu deze discretisatie van $$ -\frac{\partial^2 u}{\partial x^2}-\frac{\partial^2 u}{\partial x^2} + V(x, y) u $$ als $M \cdot v$. Hierbij moet je de matrix $M$ bepalen aan de hand van de discretisatie.
|
|
Het probleem is nu gediscretiseerd naar:
$$ M v = E v $$
voor onbekende vectoren $v$ en eigenwaarden $E$.
Bepaal de 10 kleinste eigenwaarden van deze matrix. Om (benaderde) eigenwaarden te vinden voor de schrödingervergelijking.
|
|
|
|
De exacte oplossing is:
- $3.19591806$
- $5.52674383$
- $5.52674383$
- $7.55780358$
- $8.03127195$
- $8.44458124$
- $9.92806122$
- $9.92806122$
- $11.3118171$
- $11.3118171$
|
|
Visualiseer met behulp van 'matrix_plot' de eigenfuncties horende bij de eigenwaarden. Hiervoor zal je de eigenvectoren van de matrix M terug moeten herordenen naar een 2d-grid.
|
|
Pas je code aan om gebruik te maken van een vierde orde benadering van de tweede afgeleiden. Zie wiki/Finite_difference_coefficient#Central_finite_difference. Bij de punten op het uiteinde zal je gebruik moeten maken van een tweede orde benadering.
|
|
De warmtevergelijking
$$\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2}$$
Gebruik de eindige-elementen (van tweede orde) methode om de $x$-as te discretiseren.
Gebruik daarna de trapezium regel om een oplossing te bekomen:
$u(t_{i+1}, x_j) = u(t_{i}, x_j) + \frac{h}{2}\left(\frac{u(t_{i}, x_{i-1}) - 2u(t_{i}, x_{i}) + u(t_{i}, x_{i+1})}{h^2} + \frac{u(t_{i+1}, x_{i-1}) - 2u(t_{i+1}, x_{i}) + u(t_{i+1}, x_{i+1})}{h^2}\right)$
|
|
|
|
|
|