Vraag 1
(a) 4
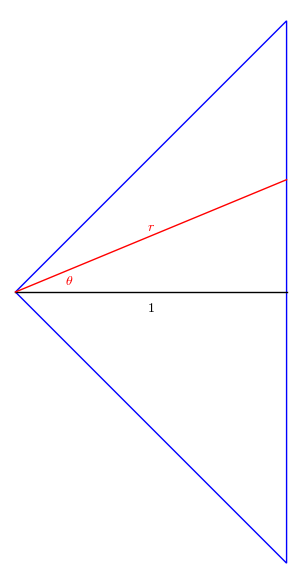
(b) Zonder twijfel varieert $\theta$ tussen $-\frac{\pi}{4}$ en $\frac{\pi}{4}$.
Met behulp van de definitie van $\cos$ kunnen we een formule voor $r$ bepalen:
|
Uit de figuur leiden we af dat: $\cos(\theta) = \frac{1}{r}$. Dus:
$$r(\theta) = \frac{1}{\cos(\theta)}\text{ met }-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}$$
(c) De oppervlakte van deze driehoek $\Delta$ wordt nu gegeven door:
$$\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \int_{0}^{\frac{1}{cos(\theta)}} r\,dr\,d\theta$$
Deze extra $r$ verschijnt door de transformatie naar poolcoördinaten.
|
|
|
|
|
|
Dus $1$. Dit komt overeen met ons resultaat uit vraag (a).
Vraag 2
Als eerste simuleren we één dobbelsteenworp ter controle:
|
|
Daarna berekenen we de som van $n$ stenen $5000$ keer.
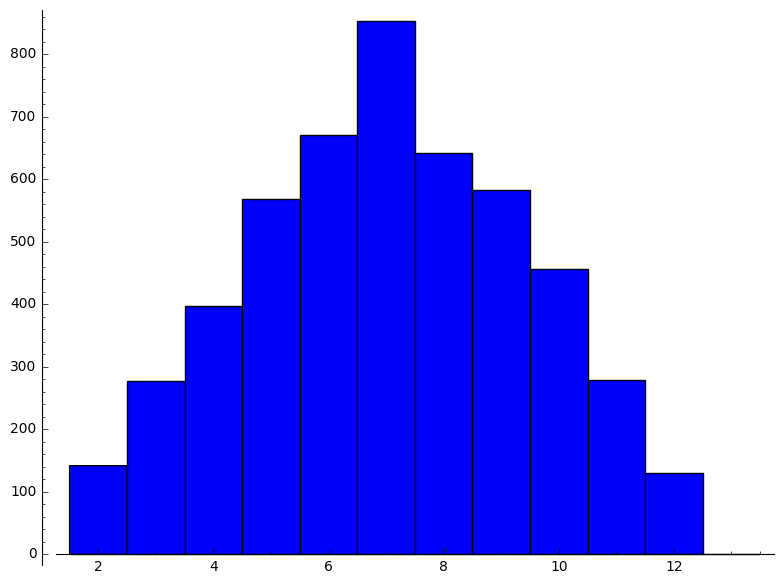
|
Dit kunnen we nu voor alle gevraagde paren van $n$ en $k$.
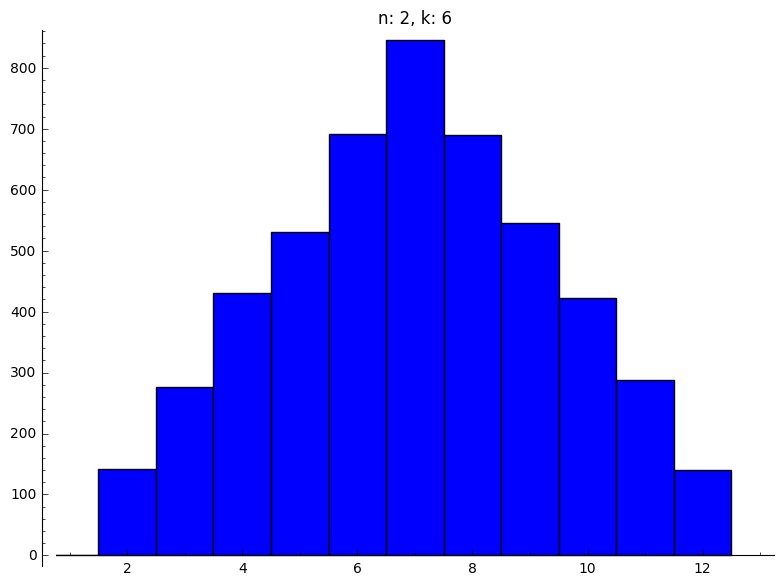 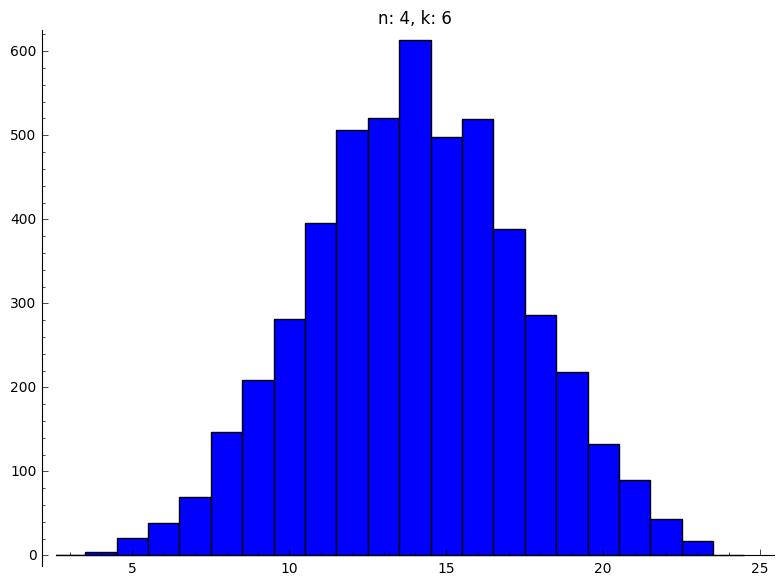 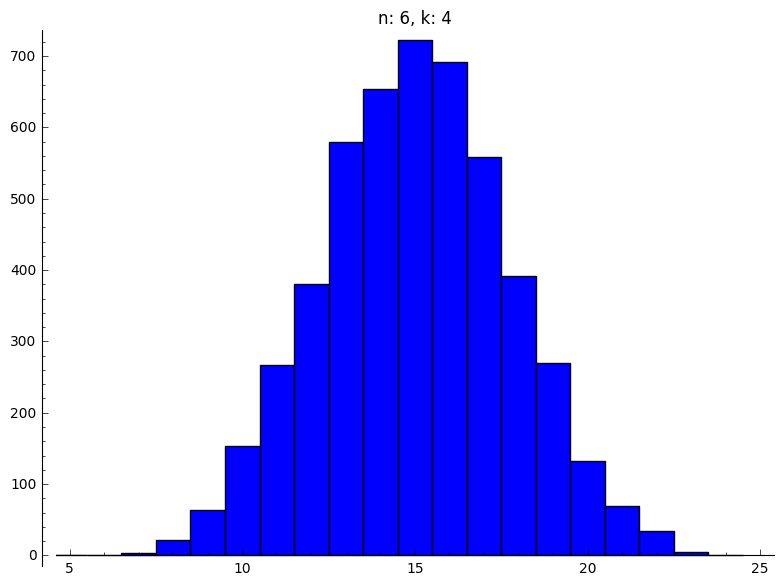 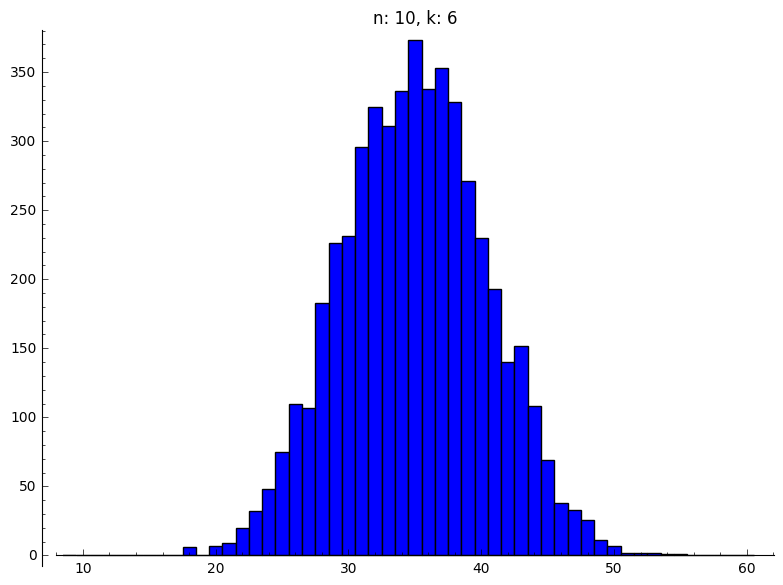 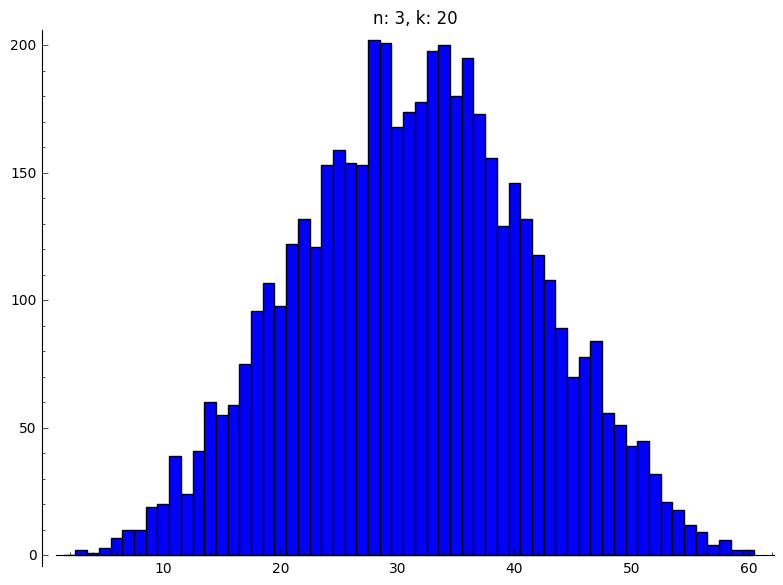
|
(b) Hier gebruiken we dezelfde plots, maar we voegen een normale verdeling toe:
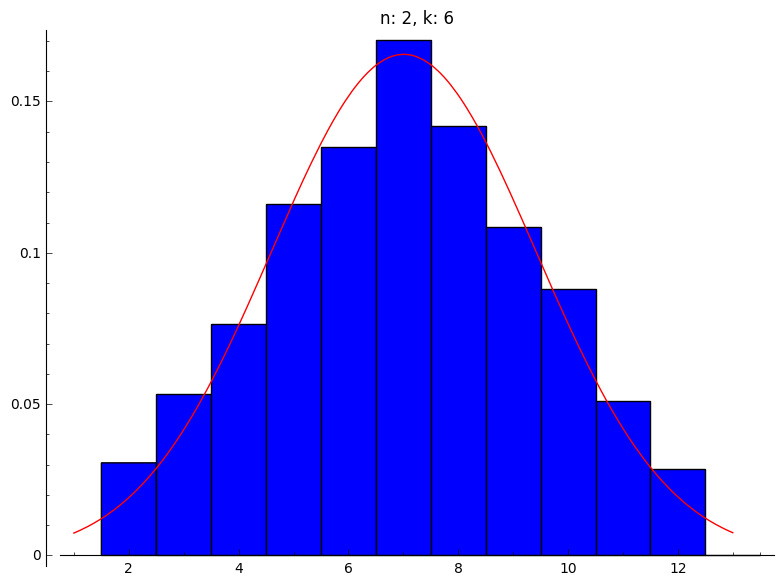 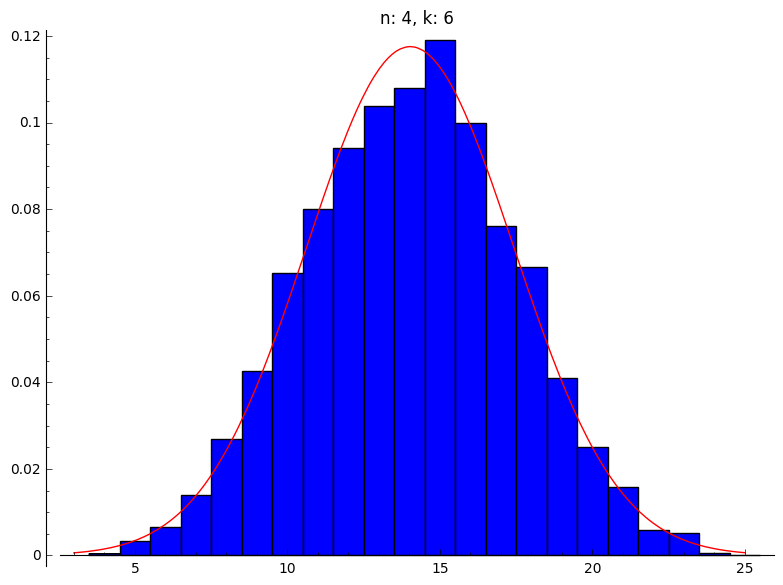 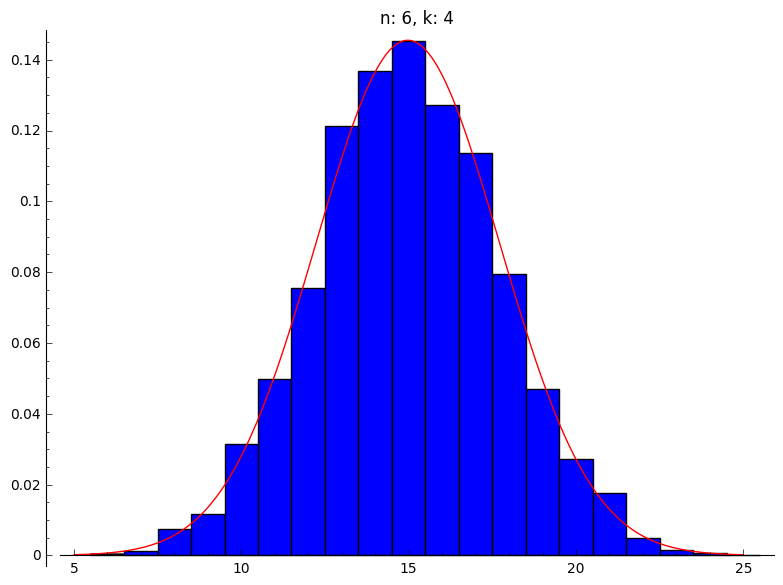 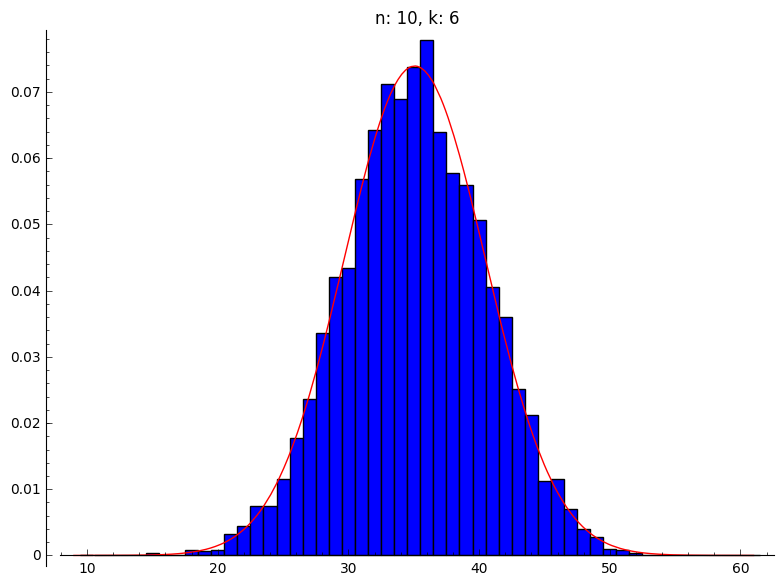 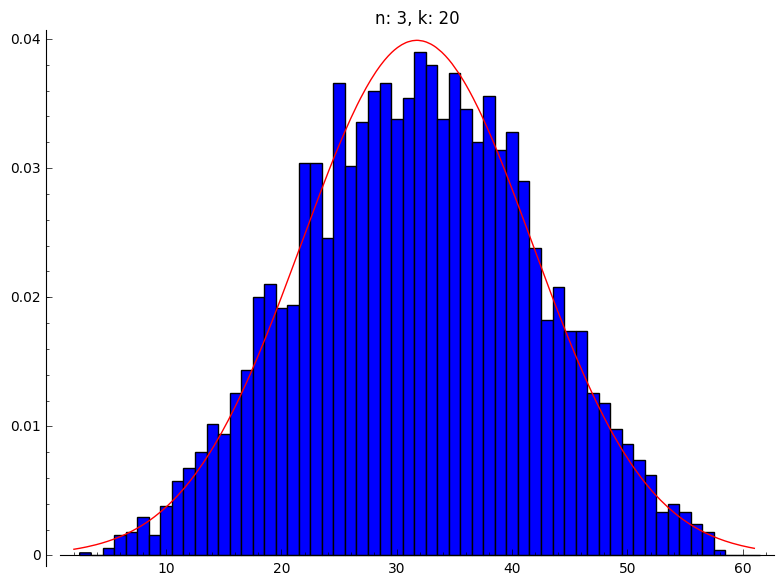
|
Vraag 3
(a) De krachten die werken op het deeltje zijn:
De eerste (horizontale) veer: $\Bold{F_1} = (1-L_1)\frac{1}{L_1}\left(\begin{array}{c}x - (-1)\\ y - 0\end{array}\right) $
Hierbij is $L_1$ de totale lengte van de veer $\left|\left(\begin{array}{c}x - (-1)\\ y - 0\end{array}\right)\right| = \sqrt{(1+x)^2 + y^2}$.
Dus $L_1 - 1$ is de uitwijking van deze veer. En $\frac{1}{L_1}\left(\begin{array}{c}x - (-1)\\ y - 0\end{array}\right)$ is een eenheidsvector die de richting aangeeft.
Analoog voor de tweede veer: $\Bold{F_2} = (1-L_2)\frac{1}{L_2}\left(\begin{array}{c}x - 0 \\ y - 1\end{array}\right) $
Met $L_2$ de totale lente van deze veer: $\sqrt{x^2 + (y-1)^2}$
Dus samen met $\Bold{F} = \Bold{F_1} + \Bold{F_2} = m \Bold{a} = m \Bold{x}''$ hebben we:
$$\begin{array}{rl} x''=&(1-L_1) \frac{x+1}{L_1} + (1-L_2) \frac{x}{L_2} \\ y''=&(1-L_1) \frac{y}{L_1} + (1-L_2) \frac{y-1}{L_2} \end{array}$$
(b) Dit stelsel ziet eruit als:
$$\left(\begin{array}{c}x\\x'\\y\\y'\end{array}\right) ' = \left(\begin{array}{l} x'\\(1-L_1) \frac{x+1}{L_1} + (1-L_2) \frac{x}{L_2} \\ y' \\ (1-L_1) \frac{y}{L_1} + (1-L_2) \frac{y-1}{L_2} \end{array}\right)$$
|
|
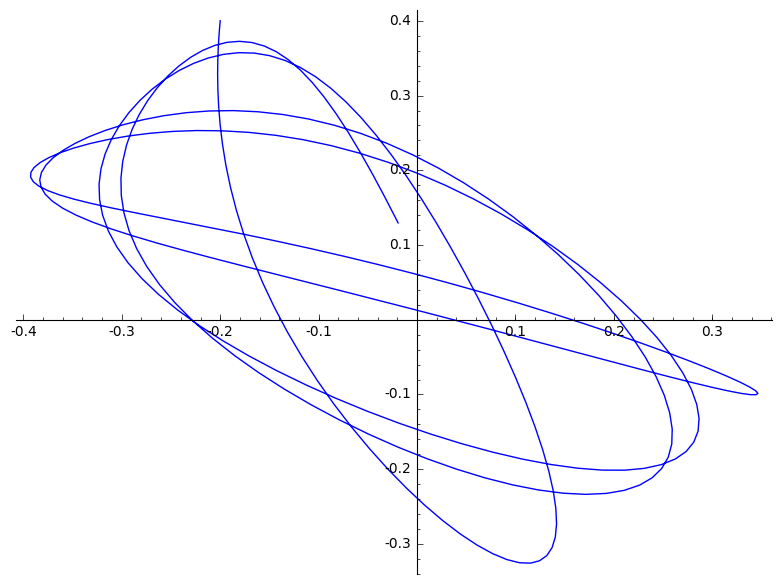
|
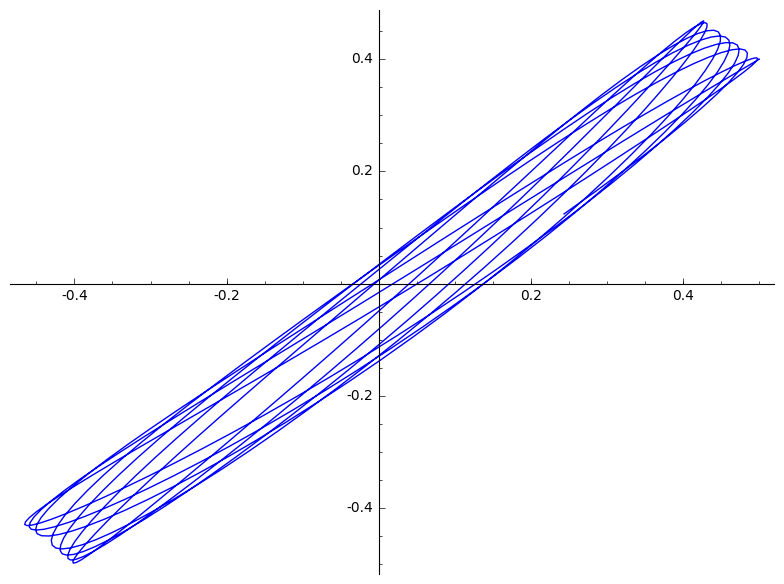
|
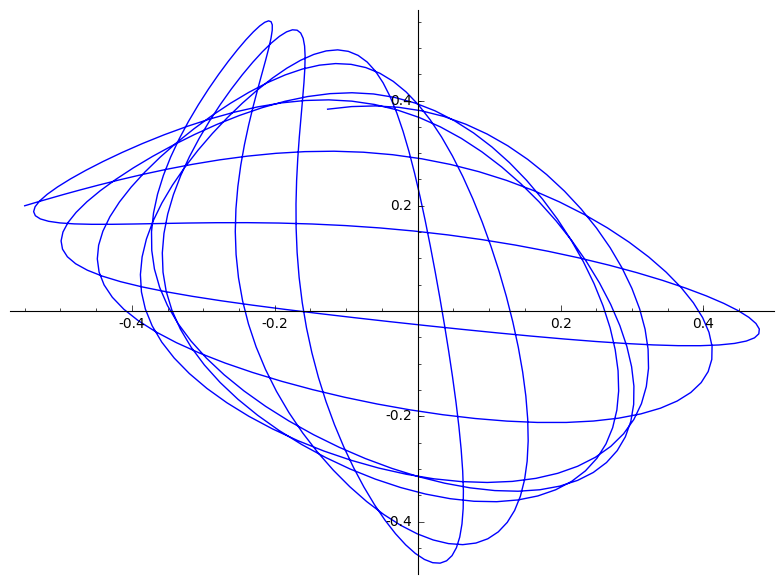
|
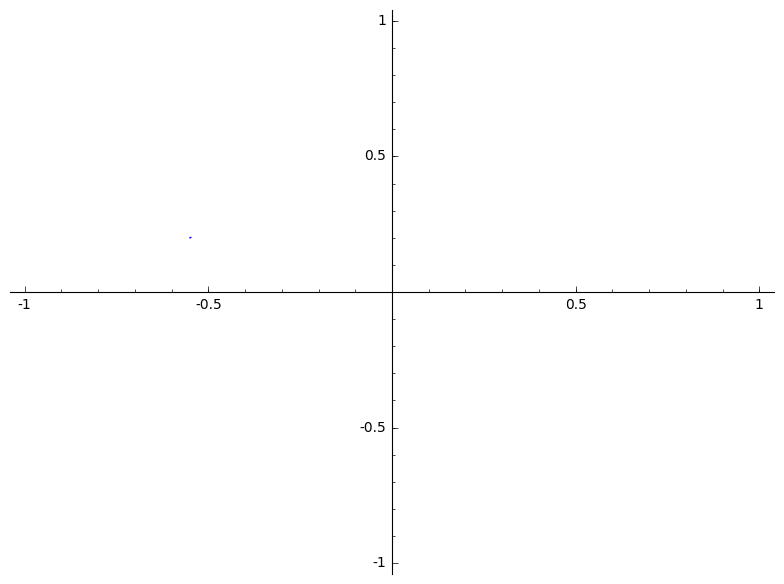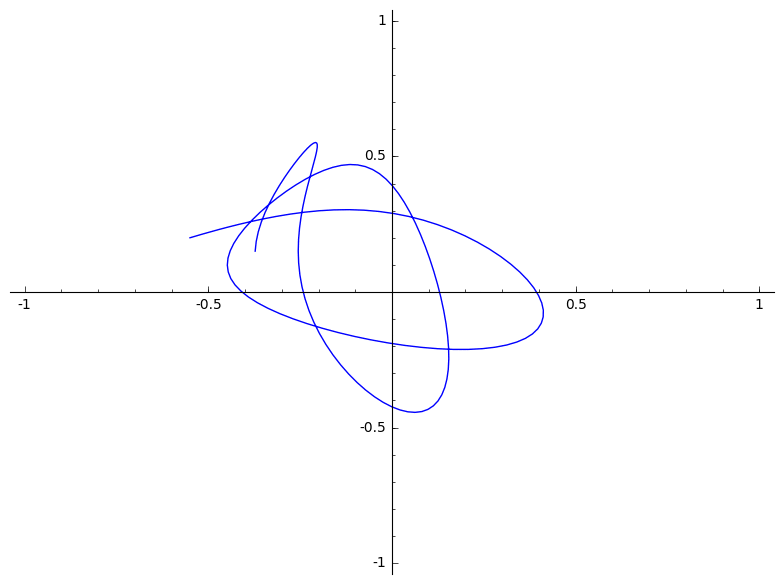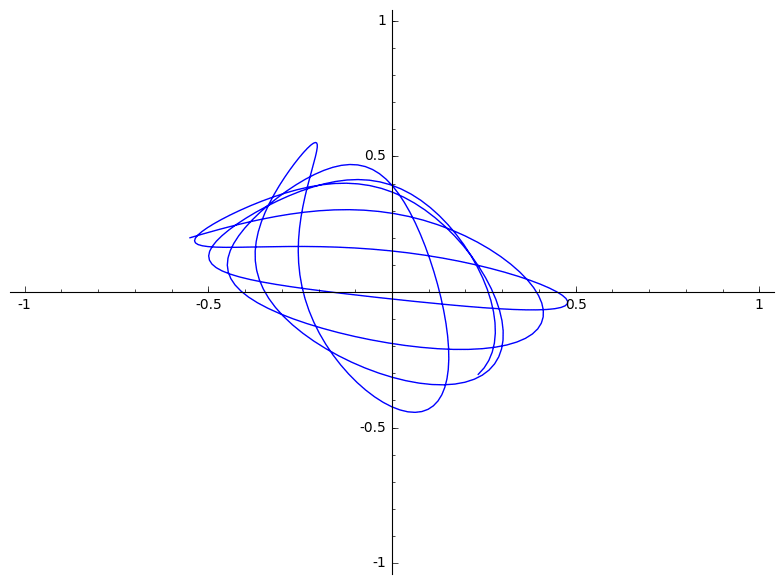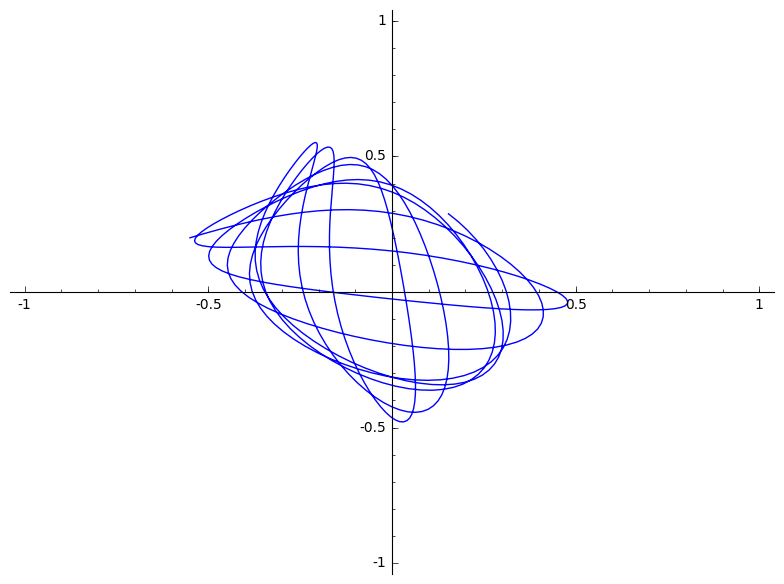
|
(d)
$(-0.5, 0.5)$ is een onstabiele evenwichtspositie. Hierdoor beweegt ons deeltje niet.
$(-0.2, 0.8)$ Zou in theorie op de lijn tussen de twee veren moeten blijven. In praktijk zorgen afrondingsfouten ervoor dat hier toch een afwijking optreedt. Deze afwijking wordt alleen maar versterkt door de onstabiliteit van deze positie.
[-0.5 0. 0.5 0. ] [-0.5 0. 0.5 0. ] [-0.5 0. 0.5 0. ] [-0.5 0. 0.5 0. ] [-0.5 0. 0.5 0. ] [-0.5 0. 0.5 0. ] [-0.5 0. 0.5 0. ] [-0.5 0. 0.5 0. ] |
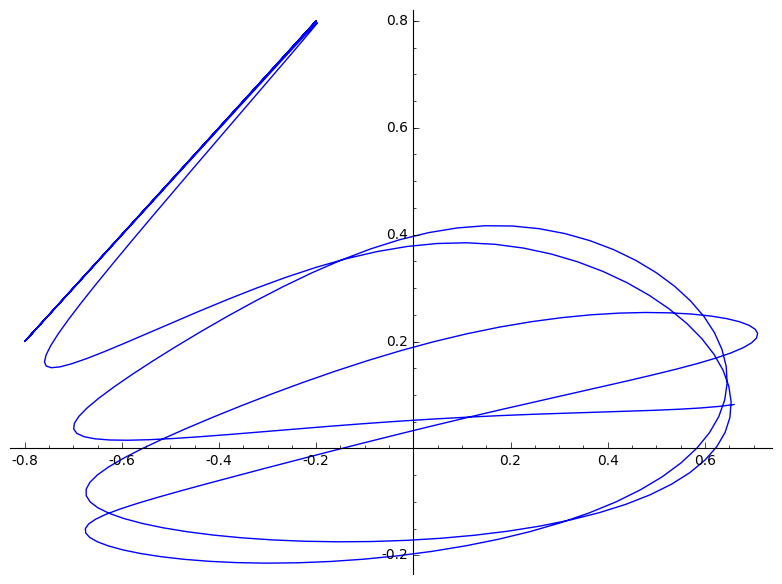
|
|
|