[CHWisGevordTech] H1 Taylorreeksen

1177 days ago by Carmen.Streat

H1: Formules van Taylor en Mac-Laurin

Voorbeeld

a) Bepaal van $f(x)=\sin{x}$ de Taylorontwikkelingen $T_3$ en $T_5$ rond $x=0$ (resp. van orde 3 en 5) .
taylor? 
       

File: /opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/calculus/functional.py

Type: <type ‘function’>

Definition: taylor(f, *args)

Docstring:

Expands self in a truncated Taylor or Laurent series in the variable v around the point a, containing terms through (x - a)^n. Functions in more variables are also supported.

INPUT:

  • *args - the following notation is supported
  • x, a, n - variable, point, degree
  • (x, a), (y, b), ..., n - variables with points, degree of polynomial

EXAMPLES:

sage: var('x,k,n')
(x, k, n)
sage: taylor (sqrt (1 - k^2*sin(x)^2), x, 0, 6)
-1/720*(45*k^6 - 60*k^4 + 16*k^2)*x^6 - 1/24*(3*k^4 - 4*k^2)*x^4 - 1/2*k^2*x^2 + 1

sage: taylor ((x + 1)^n, x, 0, 4)
1/24*(n^4 - 6*n^3 + 11*n^2 - 6*n)*x^4 + 1/6*(n^3 - 3*n^2 + 2*n)*x^3 + 1/2*(n^2 - n)*x^2 + n*x + 1

sage: taylor ((x + 1)^n, x, 0, 4)
1/24*(n^4 - 6*n^3 + 11*n^2 - 6*n)*x^4 + 1/6*(n^3 - 3*n^2 + 2*n)*x^3 + 1/2*(n^2 - n)*x^2 + n*x + 1

Taylor polynomial in two variables:

sage: x,y=var('x y'); taylor(x*y^3,(x,1),(y,-1),4)
(x - 1)*(y + 1)^3 - 3*(x - 1)*(y + 1)^2 + (y + 1)^3 + 3*(x - 1)*(y + 1) - 3*(y + 1)^2 - x + 3*y + 3

File: /opt/sage/sage-7.4/local/lib/python2.7/site-packages/sage/calculus/functional.py

Type: <type ‘function’>

Definition: taylor(f, *args)

Docstring:

Expands self in a truncated Taylor or Laurent series in the variable v around the point a, containing terms through (x - a)^n. Functions in more variables are also supported.

INPUT:

  • *args - the following notation is supported
  • x, a, n - variable, point, degree
  • (x, a), (y, b), ..., n - variables with points, degree of polynomial

EXAMPLES:

sage: var('x,k,n')
(x, k, n)
sage: taylor (sqrt (1 - k^2*sin(x)^2), x, 0, 6)
-1/720*(45*k^6 - 60*k^4 + 16*k^2)*x^6 - 1/24*(3*k^4 - 4*k^2)*x^4 - 1/2*k^2*x^2 + 1

sage: taylor ((x + 1)^n, x, 0, 4)
1/24*(n^4 - 6*n^3 + 11*n^2 - 6*n)*x^4 + 1/6*(n^3 - 3*n^2 + 2*n)*x^3 + 1/2*(n^2 - n)*x^2 + n*x + 1

sage: taylor ((x + 1)^n, x, 0, 4)
1/24*(n^4 - 6*n^3 + 11*n^2 - 6*n)*x^4 + 1/6*(n^3 - 3*n^2 + 2*n)*x^3 + 1/2*(n^2 - n)*x^2 + n*x + 1

Taylor polynomial in two variables:

sage: x,y=var('x y'); taylor(x*y^3,(x,1),(y,-1),4)
(x - 1)*(y + 1)^3 - 3*(x - 1)*(y + 1)^2 + (y + 1)^3 + 3*(x - 1)*(y + 1) - 3*(y + 1)^2 - x + 3*y + 3
f(x)=sin(x) T3=taylor(f,x,0,3) T5=taylor(f,x,0,5) show(T3) show(T5) 
        

                                
                            

                            
                                

                                    

                                

                            
                                

                                    
                                

                        

                    		
                

            

        

        


    




  
    

    
    

      
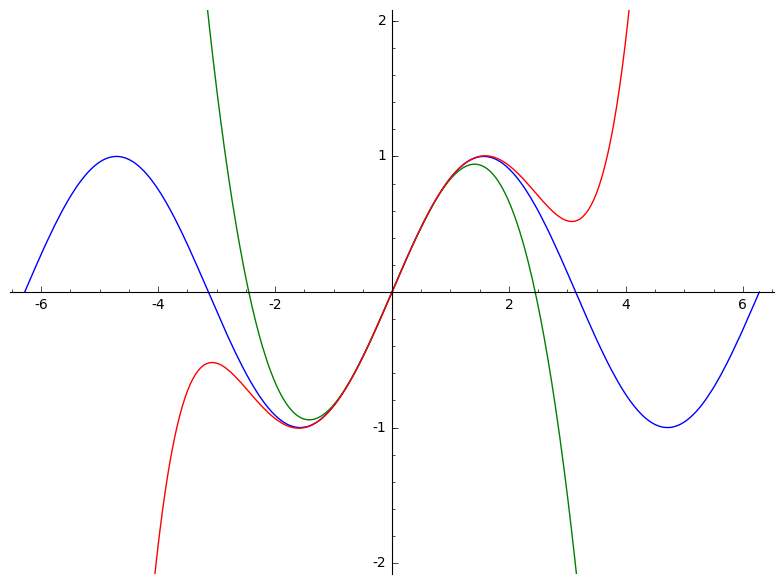
b) Teken de grafiek van $f(x)=\sin(x)$ samen met de grafieken van $T_3,T_5$ in het interval $[-2\pi,2\pi]$ (geef elke grafiek een andere kleur)

    





  
    

    
    






    


        
        
        
            
                
            
            
                
p=plot(f,(x,-2*pi,2*pi),ymax=2,ymin=-2)+plot(T3,(x,-2*pi,2*pi), color='green')+plot(T5,(x,-2*pi,2*pi), color='red')
p 

            
            

            

        

        
        
        

            

                

                    
                               
                    
                    
                        

                            

                                
                                    
                                
                            

                            
                                

                                    
                                

                            
                                

                                    
                                

                        

                    		
                

            

        

        


    




  
    

    
    

      
 


Opgave 1


Bepaal de Mac-Laurin-reeksontwikkeling van de functie $f(x)=e^{\sin(x)}$ t.e.m. termen in $x^4$. Maak gebruik van deze reeksontwikkeling om een benadering te bepalen voor $f(0.1)$. Bereken de afwijking van deze waarde t.o.v. de exacte waarde van $f(0.1)$. (oefening 1.8(b))

    





  
    

    
    






    


        
        
        
            
                
            
            
                
 

            
            

            

        

        
        
        

            

                

                    
                               
                    
                    
                        

                            

                                
                                    
                                
                            

                            
                                

                                    
                                

                            
                                

                                    
                                

                        

                    		
                

            

        

        


    




  
    

    
    

      
Opgave 2


Bepaal de Taylor-reeksontwikkeling van  $f(x)=\ln\left(\frac{3x}{1+x}\right)$  in de omgeving van  $x=\frac{1}{2}$ t.e.m. termen in $x^3.$ Gebruik deze reeksontwikkeling om een benadering te bepalen voor $f(0.6)$. Bereken de afwijking van deze waarde t.o.v de exacte waarde van $f(0.6)$. (oefening 1.8(d))

    





  
    

    
    






    


        
        
        
            
                
            
            
                
 

            
            

            

        

        
        
        

            

                

                    
                               
                    
                    
                        

                            

                                
                                    
                                
                            

                            
                                

                                    
                                

                            
                                

                                    
                                

                        

                    		
                

            

        

        


    




  
    

    
    

      
Opgave 3


a) Bepaal de Mac-Laurinreeksontwikkeling van $f(x)=\sqrt{4+x}$ t.e.m. termen in $x^6$. Teken de grafiek van $f(x)$ samen met de bekomen reeksontwikkeling voor $x \in [-4,8]$.


b) Gebruik $f(x)$ om $\sqrt{5}$ te berekenen op 10 decimalen en gebruik de reeksontwikkeling om een benadering van $\sqrt{5}$ te bepalen op 10 decimalen. Bereken (de fout) het verschil tussen de twee bekomen waarden voor $\sqrt{5}$ . Doe nu hetzelfde voor $\sqrt{10}$ (ook op 10 decimalen).


c) Probeer de benadering op 10 decimalen van $\sqrt{5}$ en van $\sqrt{10}$ te verbeteren door meer termen in de Mac-Laurin-reeks te nemen: eerst tot $x^{10}$, dan tot $x^{15}$ en tenslotte tot $ x^{20}$. Wat valt op als je de fout bekijkt? Kan je dat verklaren?


a) 

    





  
    

    
    






    


        
        
        
            
                
            
            
                
 

            
            

            

        

        
        
        

            

                

                    
                               
                    
                    
                        

                            

                                
                                    
                                
                            

                            
                                

                                    
                                

                            
                                

                                    
                                

                        

                    		
                

            

        

        


    




  
    

    
    

      
b)

    





  
    

    
    






    


        
        
        
            
                
            
            
                
 

            
            

            

        

        
        
        

            

                

                    
                               
                    
                    
                        

                            

                                
                                    
                                
                            

                            
                                

                                    
                                

                            
                                

                                    
                                

                        

                    		
                

            

        

        


    




  
    

    
    






    


        
        
        
            
                
            
            
                
 

            
            

            

        

        
        
        

            

                

                    
                               
                    
                    
                        

                            

                                
                                    
                                
                            

                            
                                

                                    
                                

                            
                                

                                    
                                

                        

                    		
                

            

        

        


    




  
    

    
    

      
c)