[Wiskundige Modellering] Epidemiologische modellen

Deel II: Epidemiologische modellen

Hoofdstuk 2: Wiskundige modellering van besmettelijke ziekten

1. Het (herschaalde) SIR-model

\[
\left\{ \begin{array}{ll}
\displaystyle \frac{d\tilde{x}}{d\tau} = -R_0\, \tilde{x}\,\tilde{y} & \tilde{x}(0) = \frac{N-1}{N} \approx 1 \\[2mm]
\displaystyle\frac{d\tilde{y}}{d\tau} =R_0\, \tilde{x}\,\tilde{y} -\tilde{y} \qquad & \tilde{y}(0)=\frac{1}{N} \approx 0 \\[2mm]
\displaystyle\frac{d\tilde{z}}{d\tau} = \tilde{y} & \tilde{z}(0)=0 \,.
\end{array} \right.\]

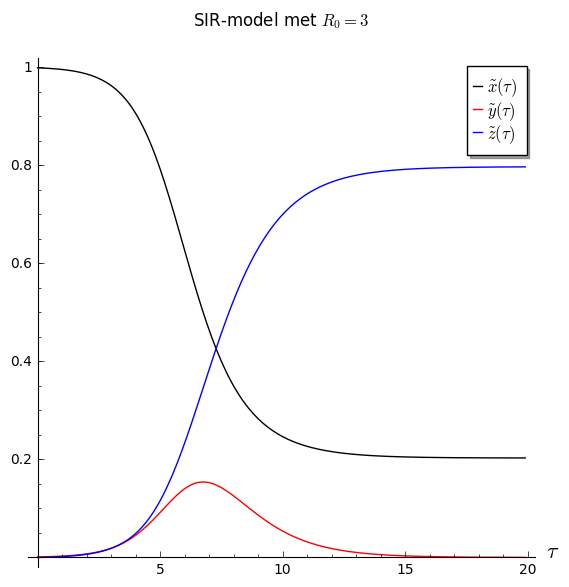
SIR-model:  Verloop van de oplossing in functie van de tijd voor een specifieke waarde van $R_0$.

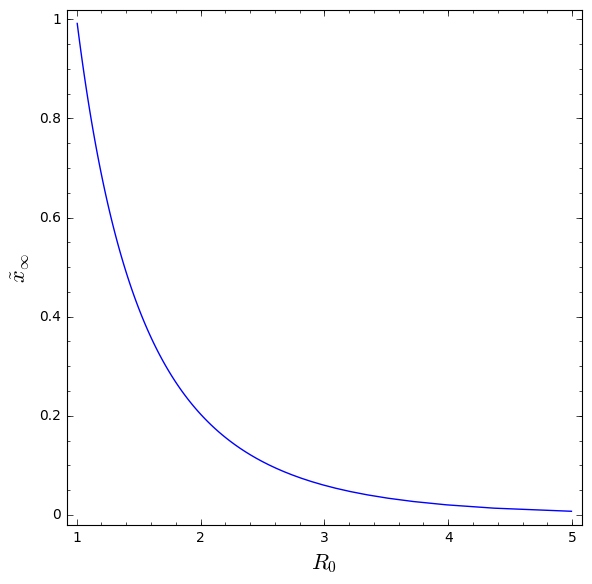
Het (herschaalde) SIR-model: resterende fractie van vatbare personen als functie van $R_0$.

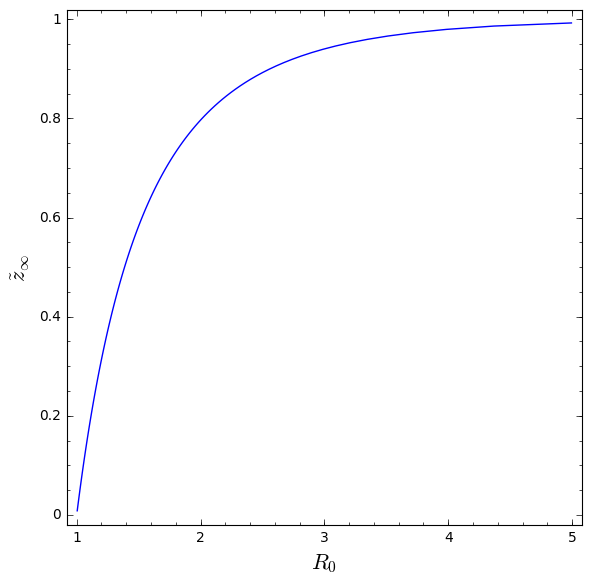
Het herschaalde SIR-model:  plot van de fractie personen die de ziekte heeft opgelopen na afloop van epidemie als functie van $R_0$

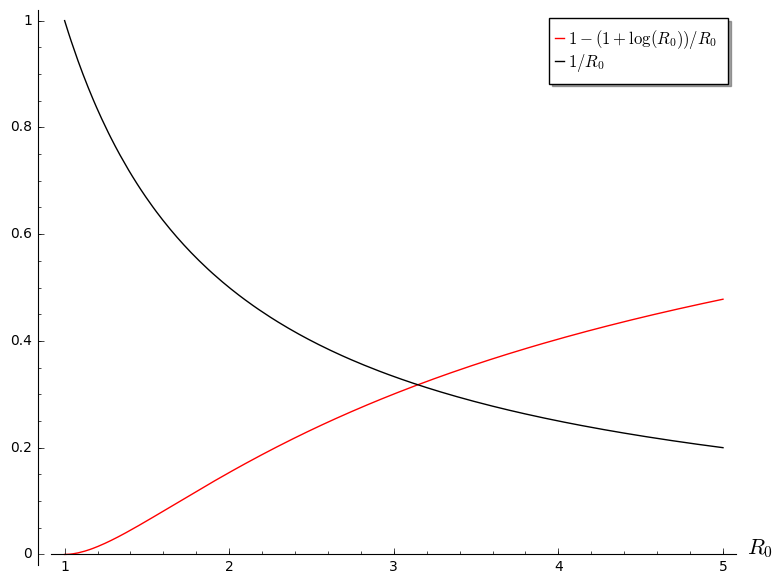
Het (herschaalde) SIR-model: Plot van de maximale graad van infectie en corresponderde maximale graad van vatbaarheid als functie van $R_0$

Het herschaalde SIR-model: verloop van de oplossing in het ($\tilde{x}$, $\tilde{y}$)-vlak voor verschillende waarden van $R_0$. 

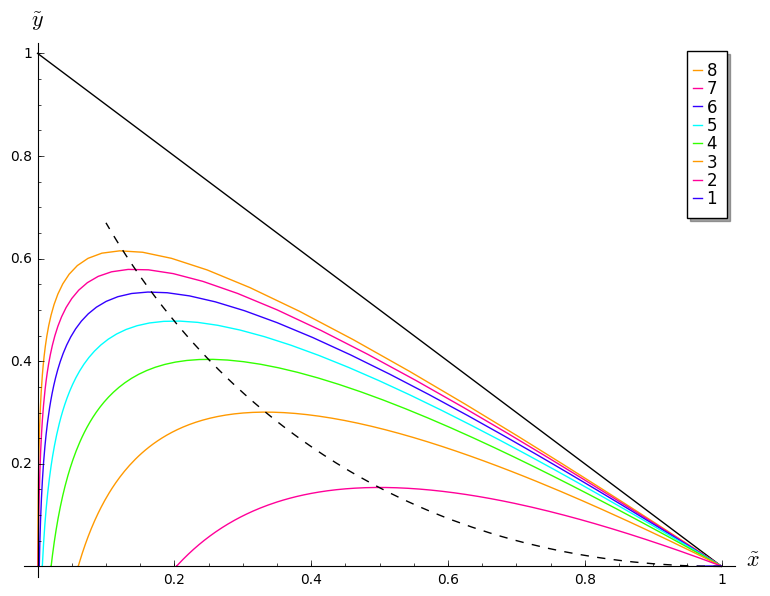
2. Het herschaalde SIRS-model

\[
\left\{ \begin{array}{ll}
\displaystyle \frac{d\tilde{x}}{d\tau} = -\frac{\beta}{\gamma}\, \tilde{x}\,\tilde{y} + \frac{\omega}{\gamma}\,\tilde{z} \qquad & \tilde{x}(0) = \frac{N-1}{N} \approx 1 \\[2mm]
\displaystyle \frac{d\tilde{y}}{d\tau} =\frac{\beta}{\gamma}\, \tilde{x}\,\tilde{y} -\tilde{y} & \tilde{y}(0)=\frac{1}{N} \approx 0 \\[2mm]
\displaystyle \frac{d\tilde{z}}{d\tau} = \tilde{y} - \frac{\omega}{\gamma} \tilde{z}& \tilde{z}(0)=0 \,.
\end{array} \right. \]

Het (herschaalde) SIRS-model: studie van de stabiliteit van de evenwichtspunten

Het (herschaalde) SIRS-model: Verloop van de oplossing in functie van de tijd voor specifieke waarden van $R_0=\beta/\gamma$ en $om= \omega/\gamma$

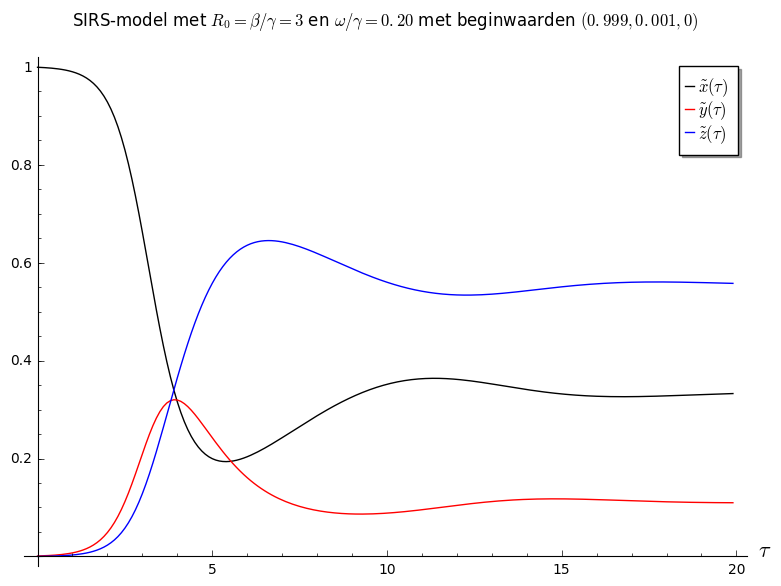
Het (herschaalde) SIRS-model: Verloop van de oplossing in het ($\tilde{x}$, $\tilde{y}$)-vlak voor verschillende waarden van $R_0=\beta/\gamma$ en vaste $\omega/\gamma$

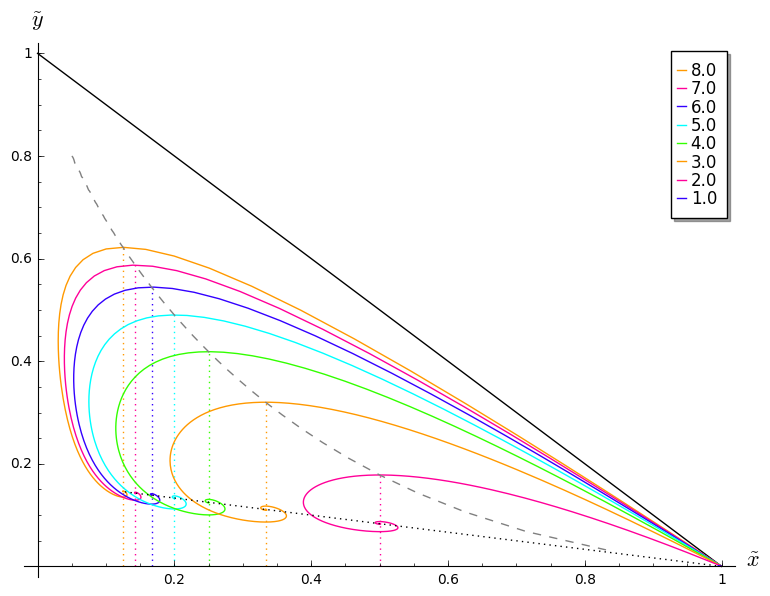
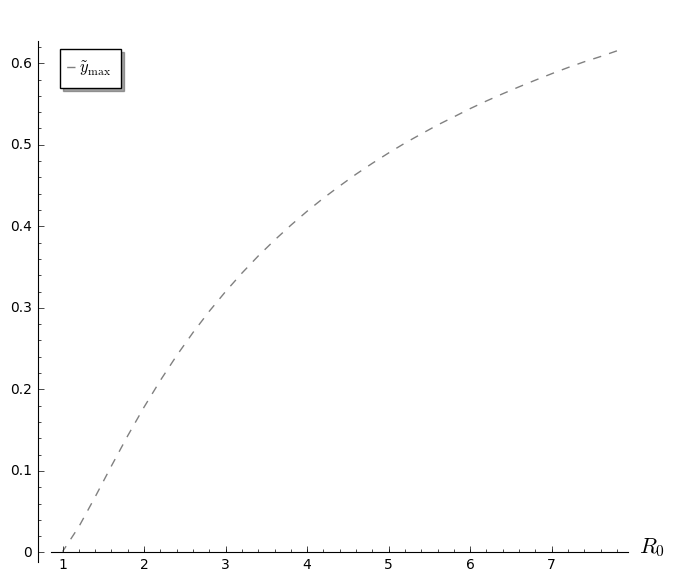
Het (herschaalde)  SIRS-model: Maximale waarde $\tilde{y}_{\rm max}$ als functie van $R_0=\beta/\gamma$ voor verschillende waarden van $\omega/\delta$

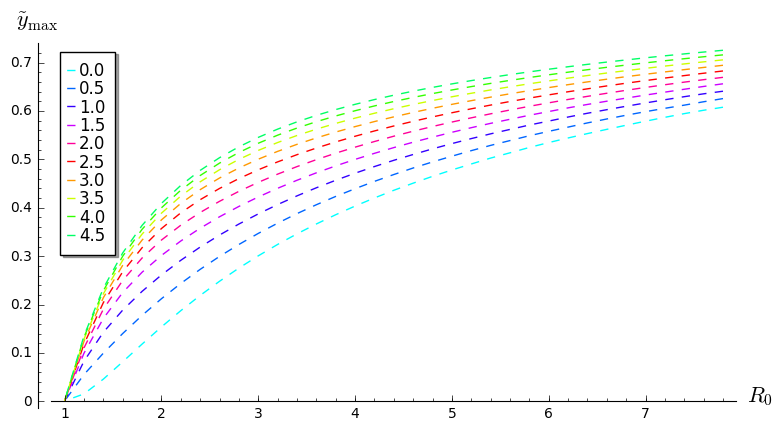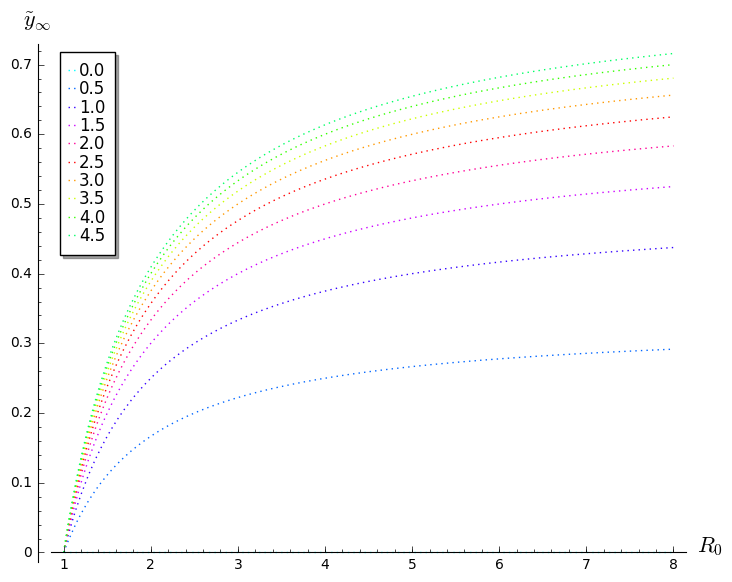
3. Het (herschaalde) SIR-model met demografie

\[
\left\{ \begin{array}{l}
\displaystyle \frac{d\tilde{x}}{d\tau} = \frac{\mu}{\gamma} -\frac{\beta}{\gamma}\, \tilde{x}\,\tilde{y} - \frac{\mu}{\gamma}\,\tilde{x} \\[2mm]
\displaystyle \frac{d\tilde{y}}{d\tau} =\frac{\beta}{\gamma}\, \tilde{x}\,\tilde{y} - \left(1+\frac{\mu}{\gamma}\right)\tilde{y} \\[2mm]
\displaystyle \frac{d\tilde{z}}{d\tau} = \tilde{y} - \frac{\mu}{\gamma} \tilde{z} \,.
\end{array} \right.\]

Het (herschaalde) SIR-model met demografie - verloop van de oplossing in functie van de tijd voor een specifieke waarde van beta/gamma en mu/gamma

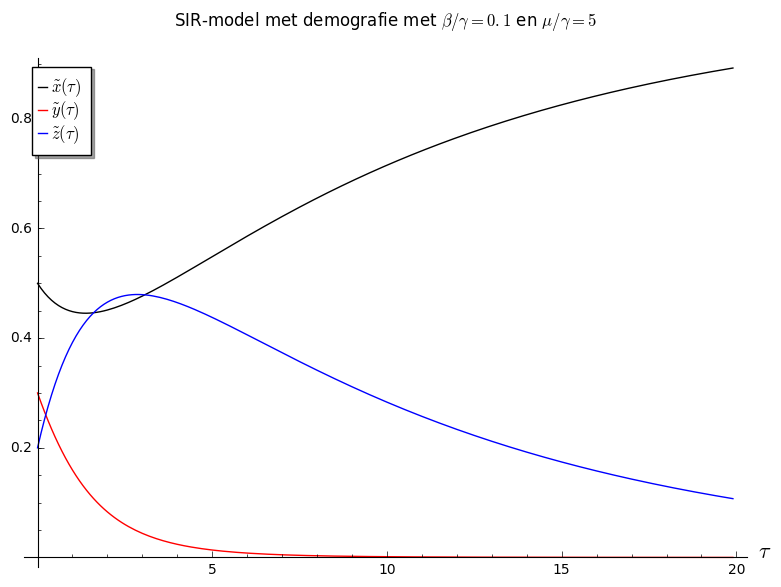
Het (herschaalde) SIR-model met demografie: Verloop van de oplossing in het  ($\tilde{x}$, $\tilde{y}$)-vlak voor verschillende waarden van $\beta/\gamma$ en $\mu/\gamma= 0.2$

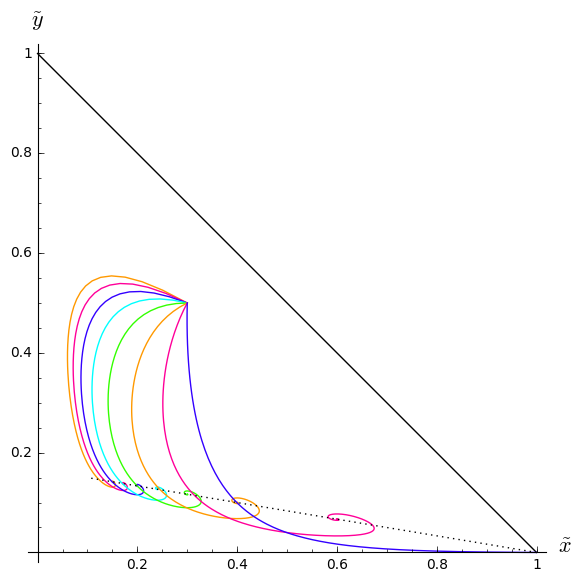
Het (herschaalde) SIR-model met demografie: studie van de stabiliteit van evenwichtspunten