Illustratie van eigenschappen van eigenwaarden en eigenfuncties van $-y''=\lambda\ y$, $y(-\pi)=y(\pi)=0$
|
|
n= var ('n')
f=function('f')(x,n)
g=function('g')(x,n)
|
|
f(x,n)=cos((2*n-1)*x/2) # lambda_n= ((2*n-1)/2)^2, n=1,2,3,...
g(x,n)=sin(n*x) # lambda_n= n^2, n=1,2,3,...
|
|
p=plot([]);
colorlist=['black','darkgray','darkblue','lightblue','darkgreen','green','brown','pink','red','orange']
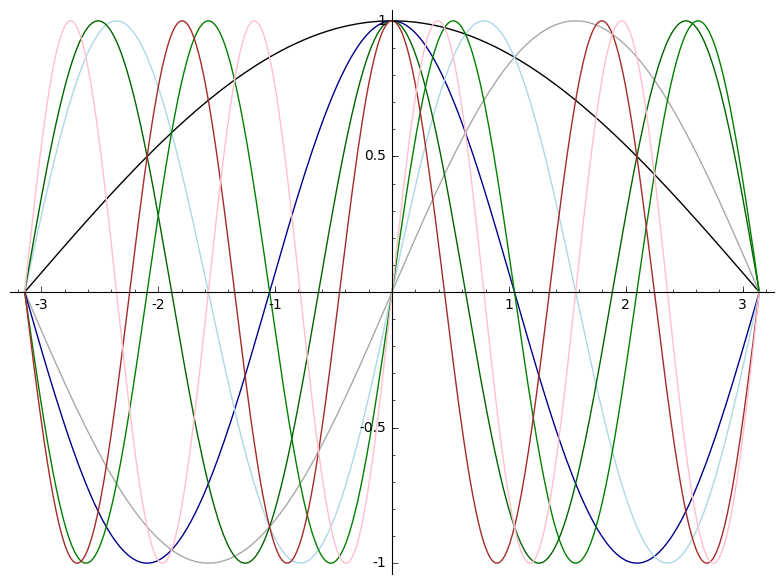
for i in range(4):
p+=plot(f(x,i+1),(x,-pi,pi),color=colorlist[2*i])
p+=plot(g(x,i+1),(x,-pi,pi),color=colorlist[2*i+1])
show(p)
|
p=plot([]);
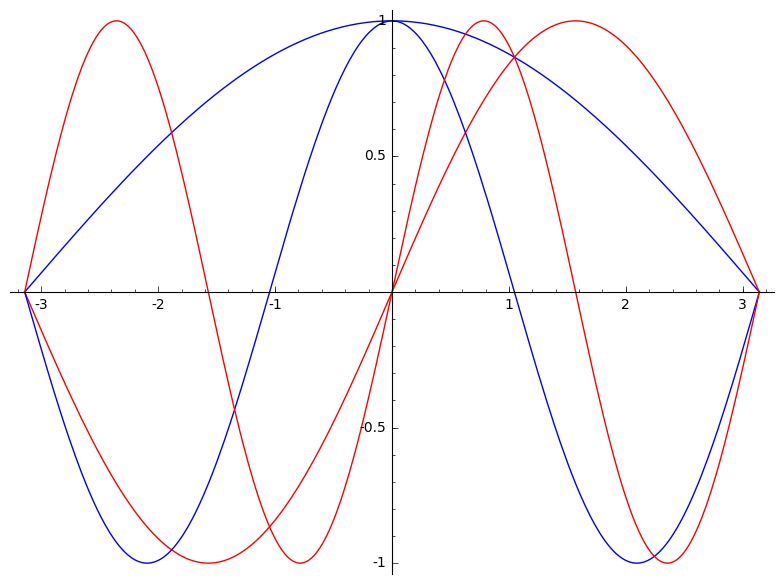
for i in range(2):
p+=plot(f(x,i+1),(x,-pi,pi),color='blue')
p+=plot(g(x,i+1),(x,-pi,pi),color='red')
show(p)
|
De blauwe eigenfuncties (cosinussen) hebben 0 en 2 nulpunten, de rode eigenfuncties (sinussen) hebben 1 en 3 nulpunten. Tussen elke twee nulpunten van een rode eigenfunctie (index $n$) ligt 1 nulpunt van de blauwe eigenfunctie (met index $n-1$). Tussen elke twee nulpunten van een blauwe eigenfunctie (index $n$) ligt 1 nulpunt van de rode eigenfunctie (met index $n-1$).
|
|